Dividimos por dos cifras en el divisor.
Os dejo aquí vídeos tutoriales para las aclaraciones.
Dividimos por dos cifras en el divisor.
Os dejo aquí vídeos tutoriales para las aclaraciones.
Dividimos por dos cifras en el divisor.
Os dejo aquí vídeos tutoriales para las aclaraciones.
Dividimos por dos cifras en el divisor.
Os dejo aquí vídeos tutoriales para las aclaraciones.

1. Práctica, Práctica y Más Práctica
Para aprender matemáticas hay que ponerse el mono de trabajo y lanzarse a hacer ejercicios matemáticos. Cuanto más se practique, mejor. Cada ejercicio tiene sus particularidades y nada mejor que los «problemas» cotidianos y cercanos.
2. Revisar los Errores
Al practicar con ejercicios, es muy importante comprobar los resultados y, más importante aún, detenerse en la parte que se ha fallado y examinar el proceso en detalle hasta asimilarlo. De nada sirve comparar resultados si no se sabe en qué se ha equivocado. De esta manera, se evitará cometer los mismos fallos en el futuro.
3. Dominar los Conceptos Clave
Dominar los conceptos importantes y el proceso de resolución de los problemas.
las Matemáticas son una asignatura secuencial, por lo que es importante asentar una base firme dominando los conceptos clave y teniendo claras las fórmulas matemáticas esenciales (lectura comprensiva, planteamiento y resolución aplicando correctamente las operaciones necesarias sin errar).
4. Consultar las Dudas
Ante el atasque en una parte de un problema o que simplemente no se entienda el proceso o enunciado, hay que aclarar dudas. Es necesario romper la timidez, la vergüenza de preguntar.
El trabajo colaborativo junto a algún compañero o compañera es esencial para consultar, aclarar dudas. «Todos somos maestros».
5. Trabajar en un Ambiente de Estudio sin Distracciones
Las Matemáticas son una asignatura que requiere más concentración que ninguna otra. Un ambiente de estudio adecuado y libre de distracciones es el factor determinante para conseguir resolver problemas.
7. Aplicar Problemas al Mundo Real
En la medida de lo posible, se intenta aplicar los ejercicios al mundo real.
Se podría hablar mucho más sobre los procesos de cualquier trabajo y aprendizaje. Os he hecho un breve resumen, y en especial sobre las matemáticas, pero todo es aplicable a todo y como les suelo decir, las matemáticas no se encuentran aisladas de las ciencias, las artes o la lengua, se podría resumir en que el conjunto es la «vida misma con sus momentos peculiares».
LA GEOMETRÍA Y LAS MEDIDAS
Conocéis muchos de los resultados, pero lo importante es el proceso de cómo llegar a ese fin.
«UN TRABAJO A REALIZAR» O «UN PROBLEMA»
Ya conocen mucha información, previamente investigada, sobre la geometría, los cuerpos geométricos, algunos conceptos, sus elementos y características. Es necesario conocer y dominar la medida de longitud, el uso de la regla, medir, trazar líneas rectas, paralelas, perpendiculares. No nos olvidamos de la necesidad de la división para averiguar las medidas exactas y otros conceptos más.
Por grupos de trabajo de investigación deben:

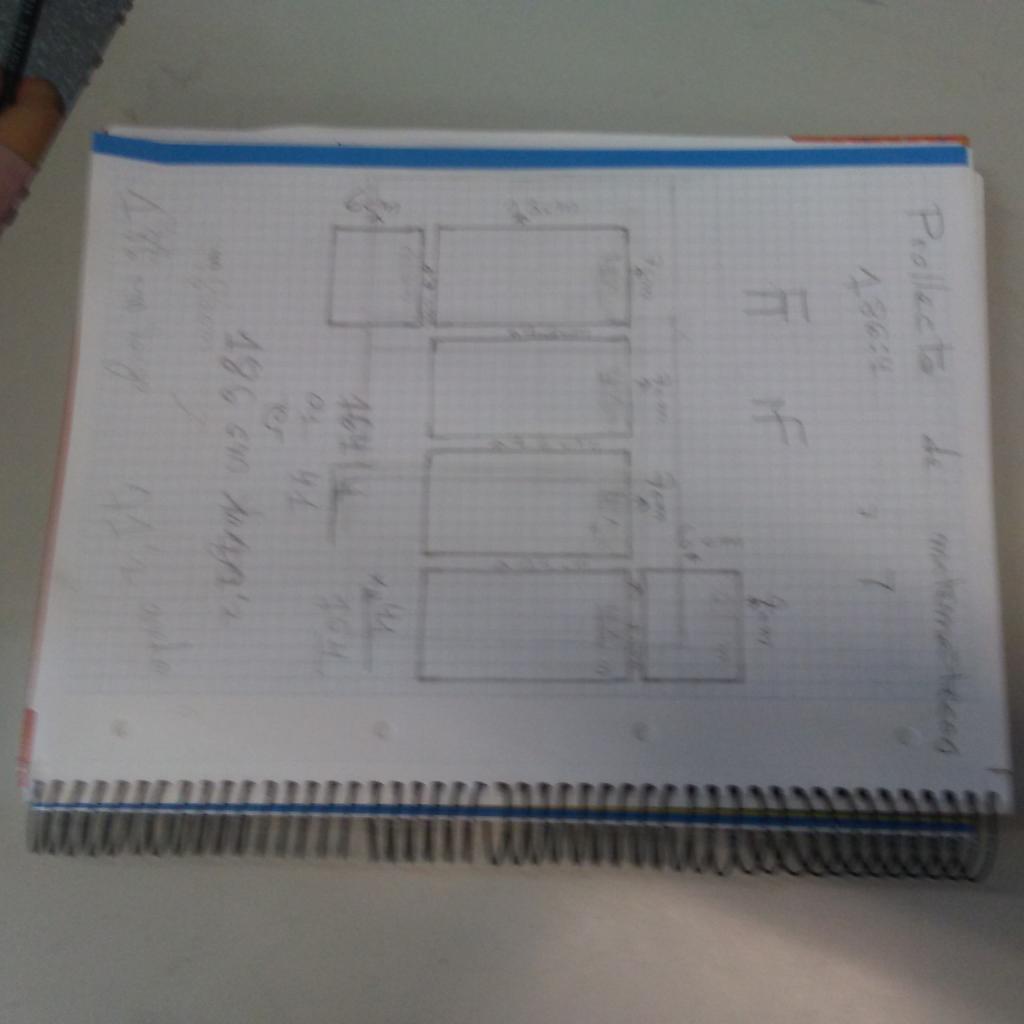 Realizar un diseño desplegable. Boceto en la libreta con las medidas a escala.
Realizar un diseño desplegable. Boceto en la libreta con las medidas a escala.
 desplegable. Aparecen dificultades de largo, ancho y grosor que hay que resolver.
desplegable. Aparecen dificultades de largo, ancho y grosor que hay que resolver.
 Se pone en práctica individualmente (diseño-boceto a escala en el cuaderno).
Se pone en práctica individualmente (diseño-boceto a escala en el cuaderno).

 Una vez trazadas las figuras planas, se revisan las medidas y se cortan las figuras trazadas.
Una vez trazadas las figuras planas, se revisan las medidas y se cortan las figuras trazadas.
 revisión si hay errores. ¿Qué ha pasado?
revisión si hay errores. ¿Qué ha pasado? Montaje colaborativo.
Montaje colaborativo.

El aula es en un gran taller manipulativo y de un enorme proceso de aprendizaje.

Toda la escuela ha colaborado en un entrañable encuentro entre grupos para conmemorar el día de la paz a través de una lecturas de cuentos que nos llevan a reflexionar sobre la convivencia y el respeto a la diversidad. Cada grupo ha elaborado una frase que representa el resumen de las ideas trabajadas.
Todos juntos, hemos participado en la escucha de «El cant dels ocells» de Paul Casals a cargo del grupo de coro de la escuela y de la deliciosa música del violonchelo, tocado por Claudia E.
Las reflexiones y el trabajo para buscar la paz y la buena convivencia continúan diariamente.
Un saludo.
Juanjo
¿De cuántas maneras distintas se pueden colocar juntos, unidos al menos de uno de sus lados, cinco cuadrados del mismo tamaño? Una forma es la siguiente:
 |
A ésta y las otras posibles configuraciones se les conoce como PENTOMINÓS. En total son 12 maneras distintas de acomodar juntos, al menos de uno de sus lados, cinco cuadrados.
El pentominó es un juego de 12 piezas que conforman gran número de acertijos del tipo de los rompecabezas. Los pentominós fueron presentados al mundo matemático en 1954 por un catedrático de la Universidad del Sur de California, Solomon W. Golomb. Uno de los aspectos más sorprendentes de este juego es que se pueden acomodar todas las piezas juntas de maneras inesperadas
 Con las doce piezas del juego de pentominós se pueden plantear y resolver un gran número de problemas. Precisamente eso es lo que los ha convertido en un interesante enigma. Los pentominós nos ofrecen miles de opciones a la hora de aprender matemáticas.
Con las doce piezas del juego de pentominós se pueden plantear y resolver un gran número de problemas. Precisamente eso es lo que los ha convertido en un interesante enigma. Los pentominós nos ofrecen miles de opciones a la hora de aprender matemáticas.
Así que como a nosotros nos encantan los acertijos, los retos y la geometría… No dudamos un momento en disfrutar de la geometría de esta manera tan lúdica. ¿Os animáis a hacerlo en casa?
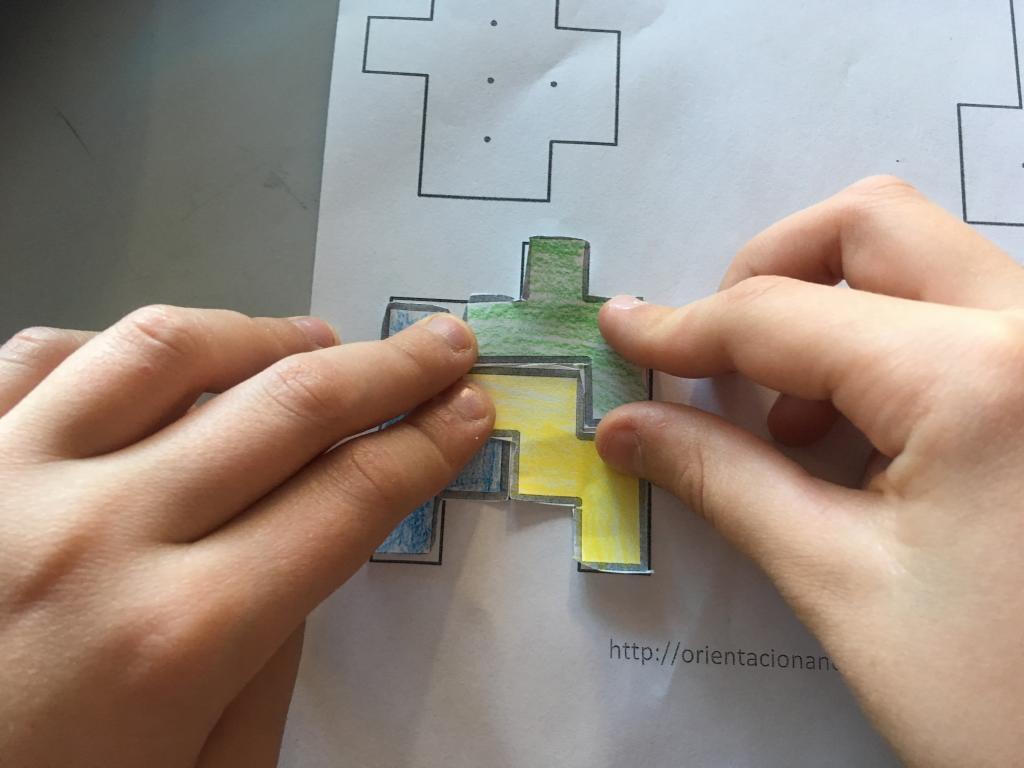
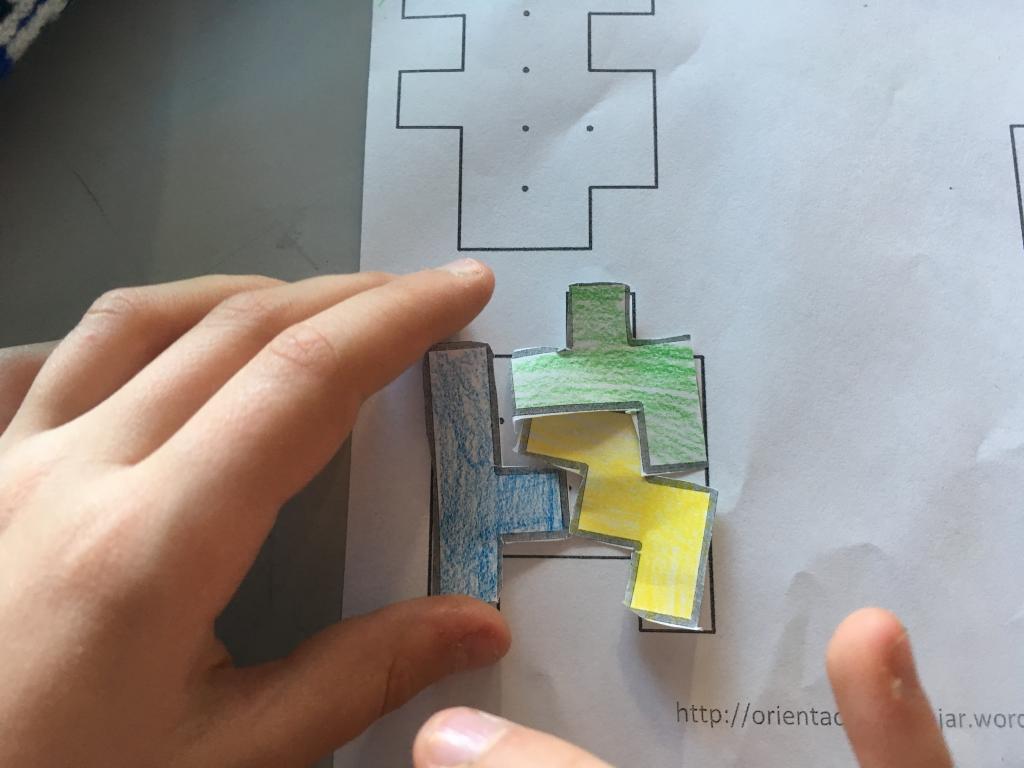
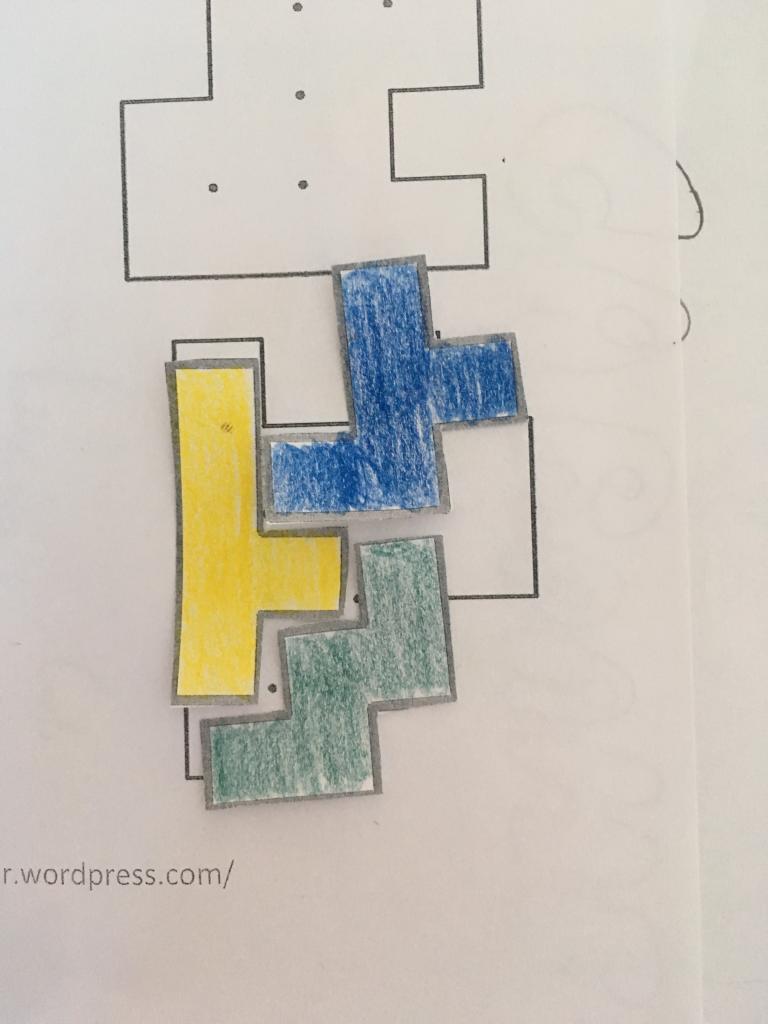
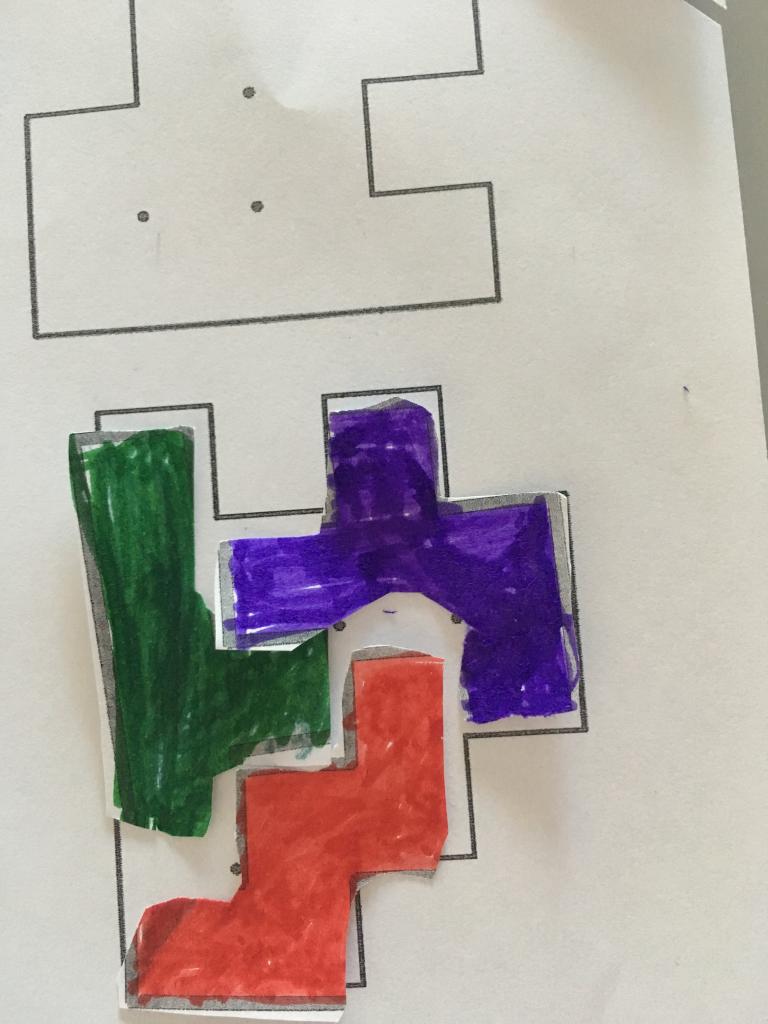
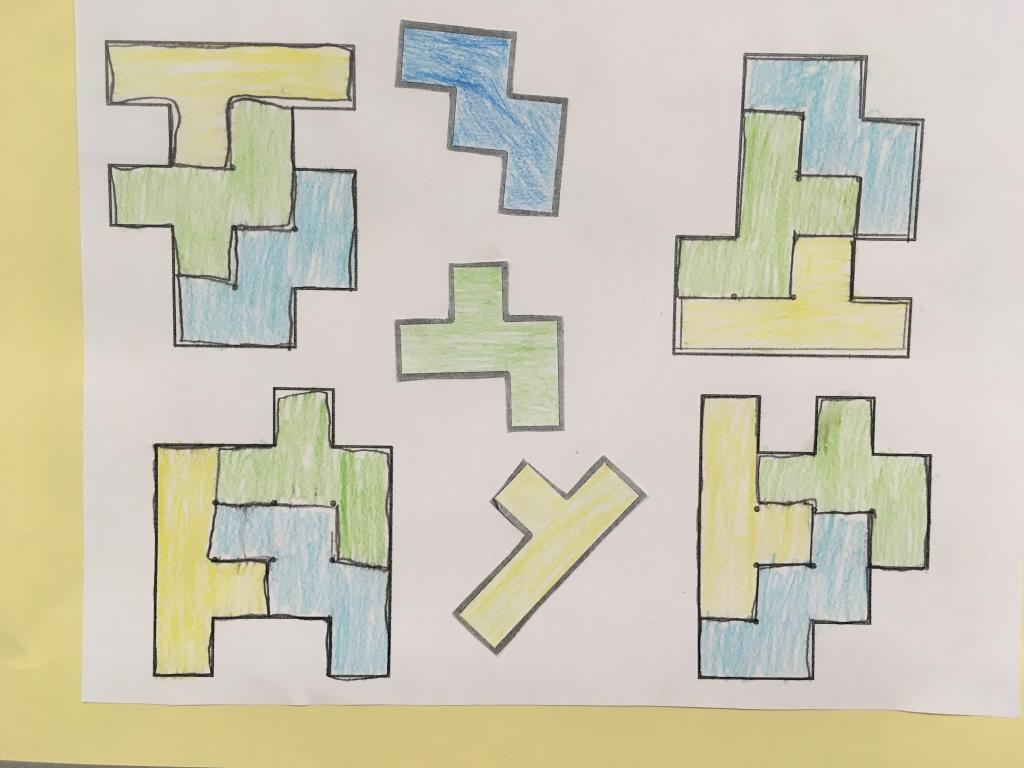

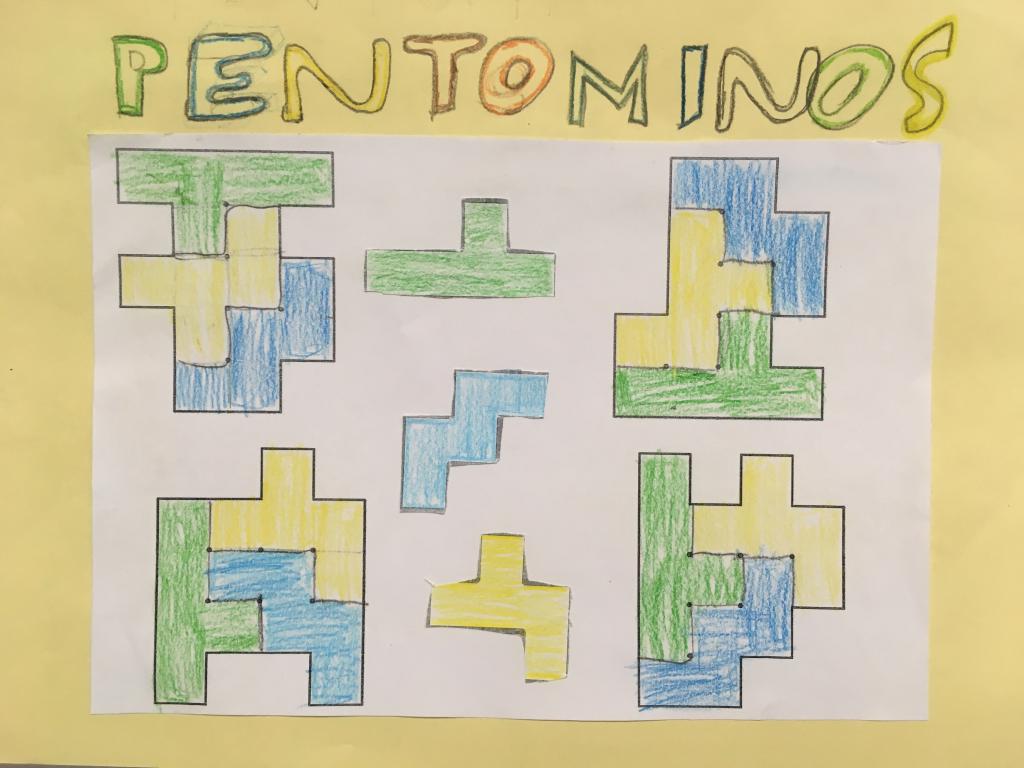

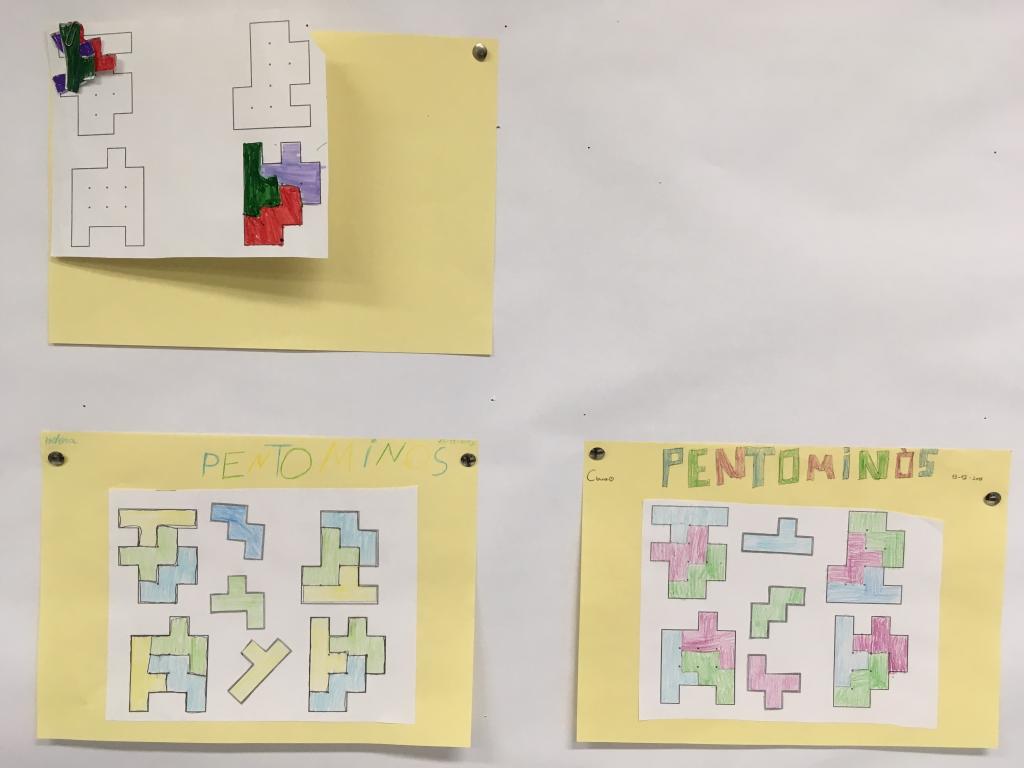
Como anécdota hay que decir que el juego Tetris está basado en los pentominós.
Buen fin de semana.
P.D.: el martes tenemos taller de cocina navideño, para ir ambientándonos.
Laura