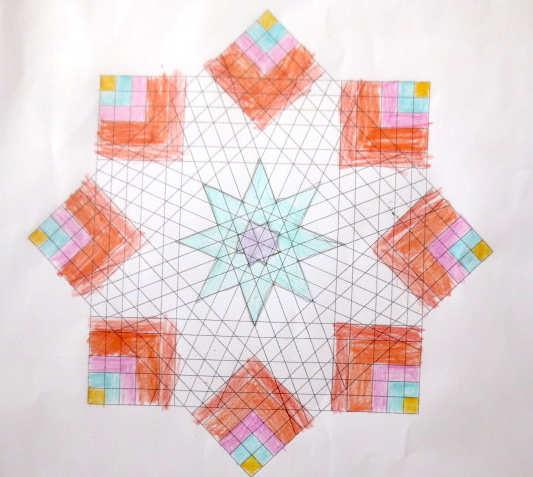
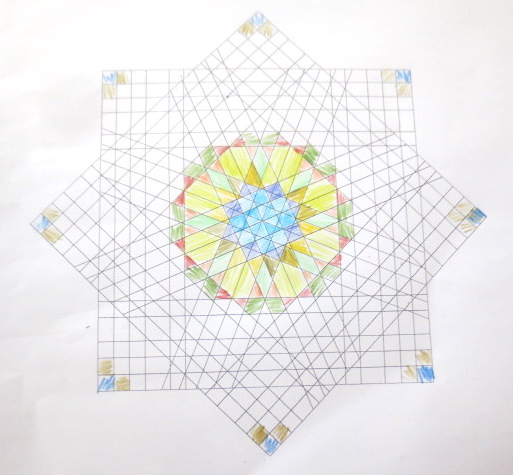
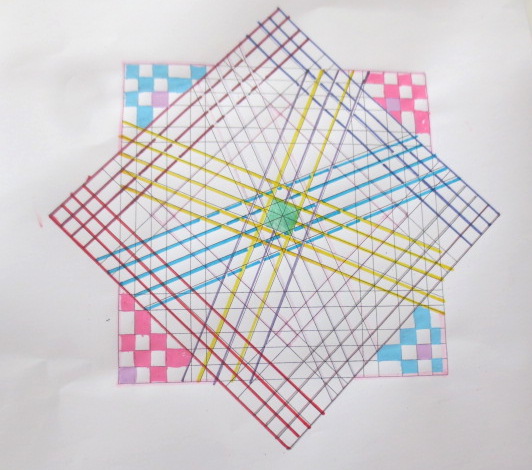
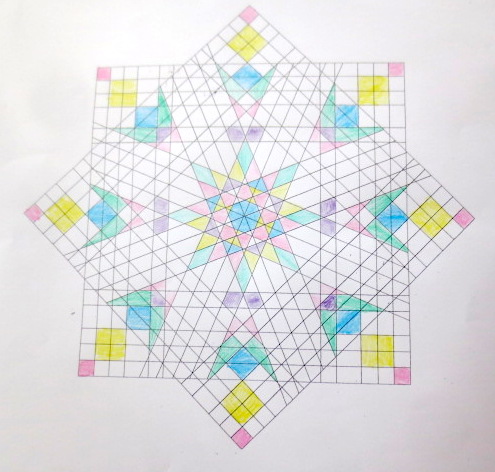
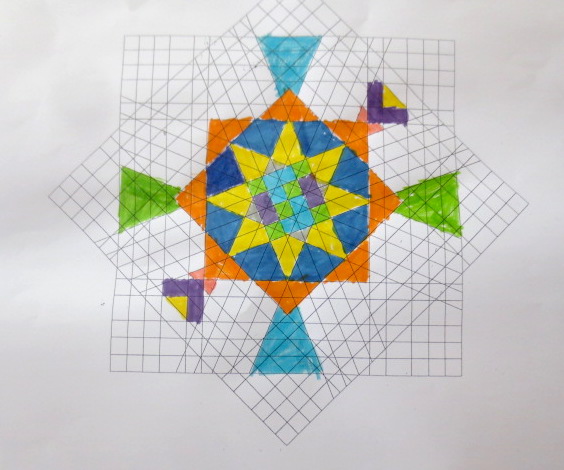
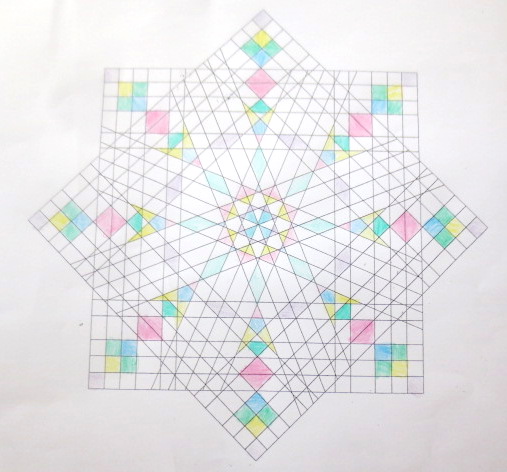
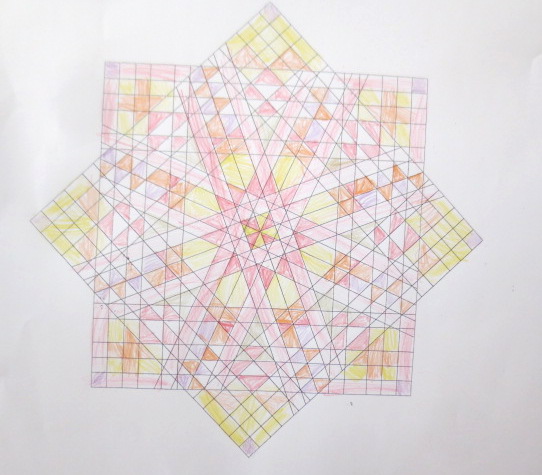
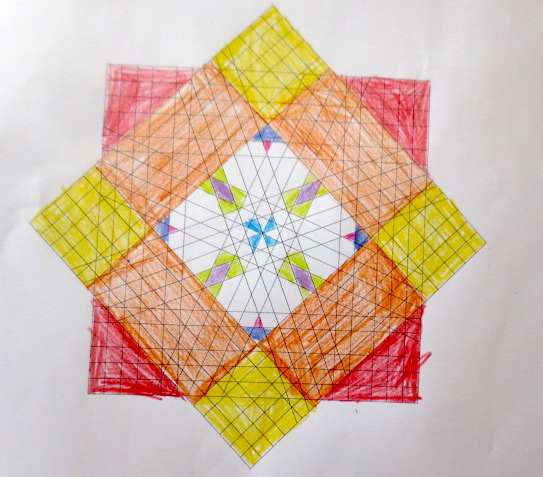
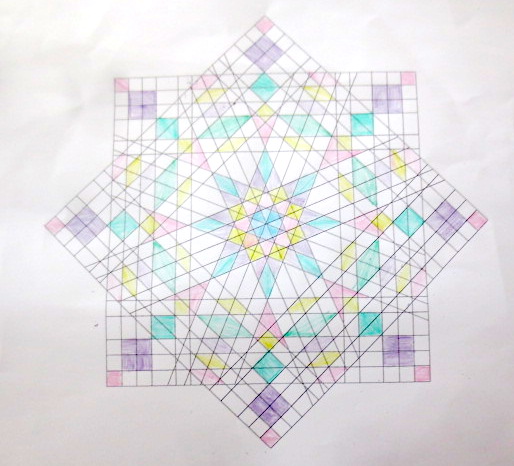
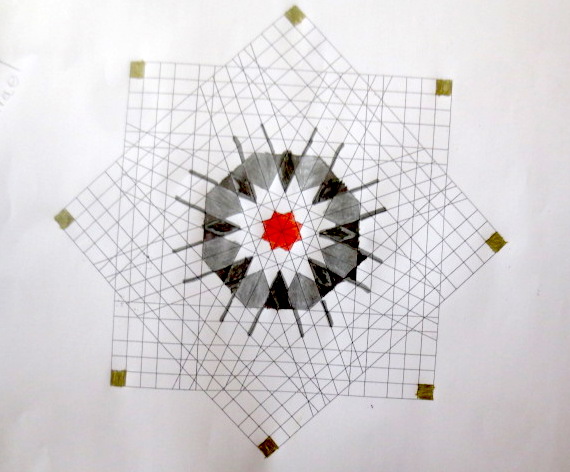
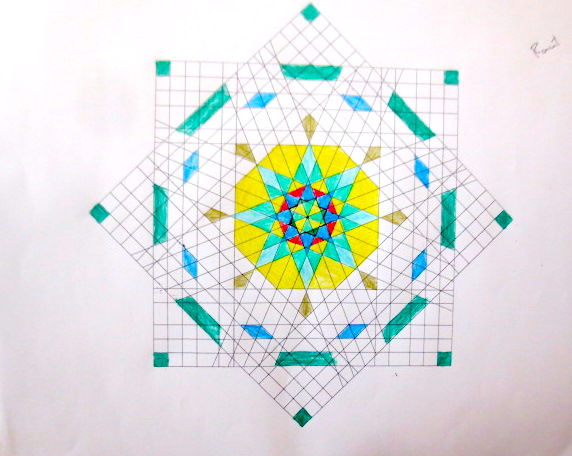
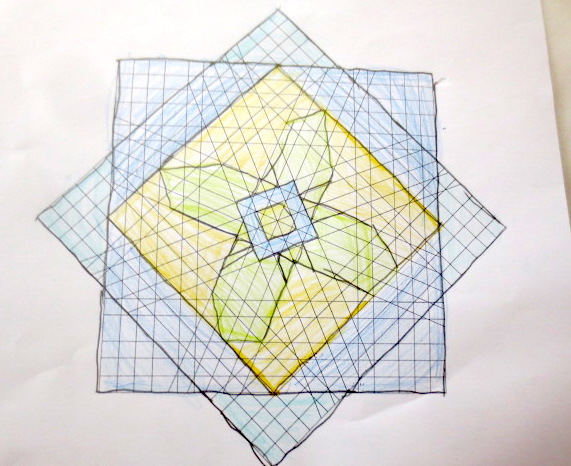
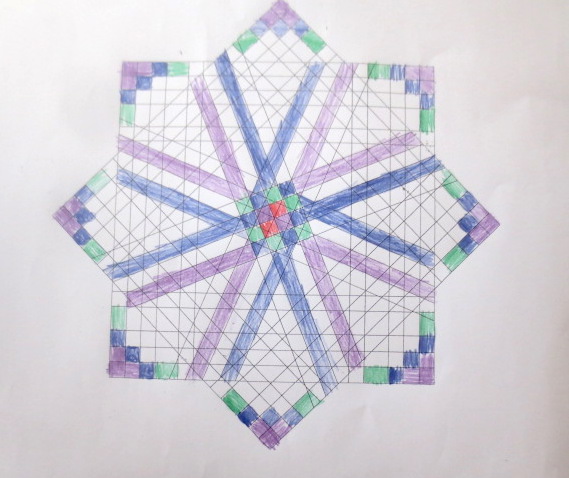
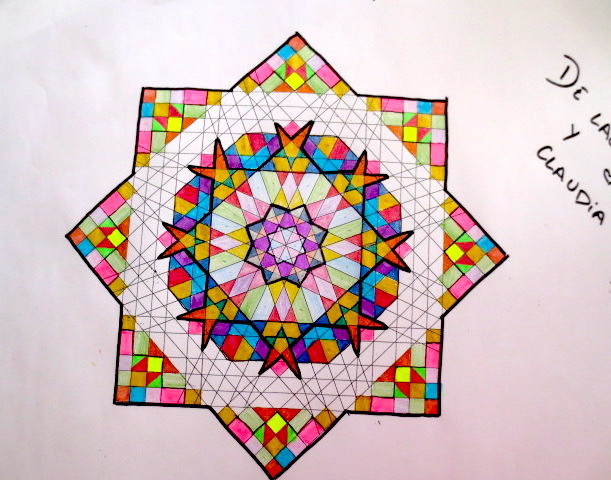
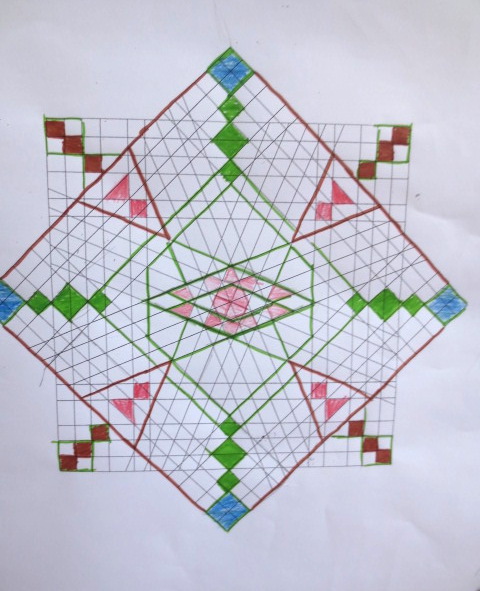
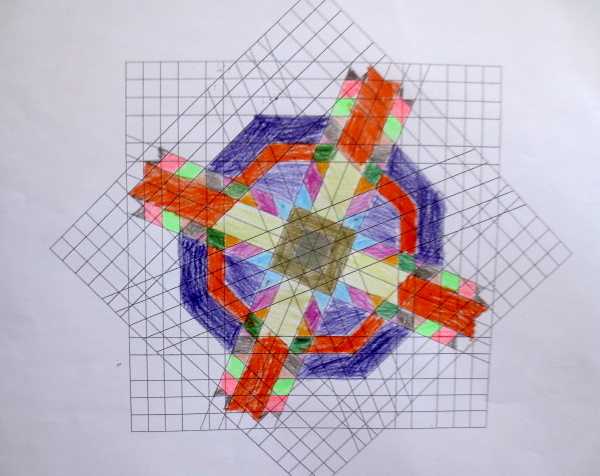
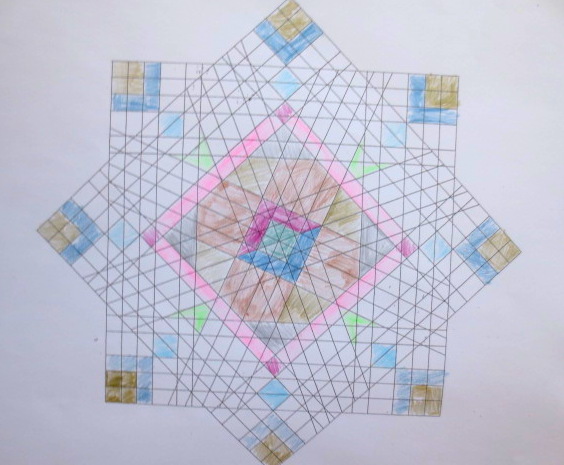
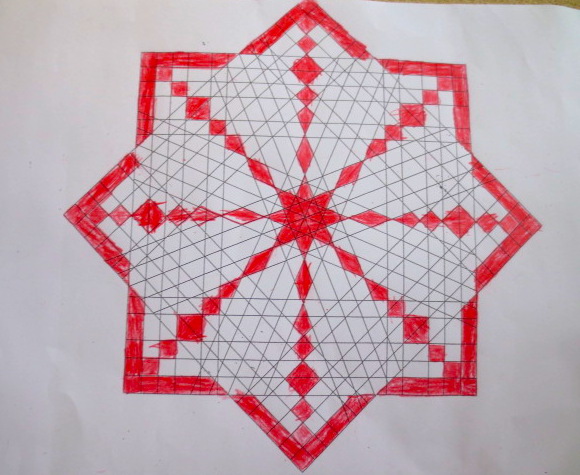
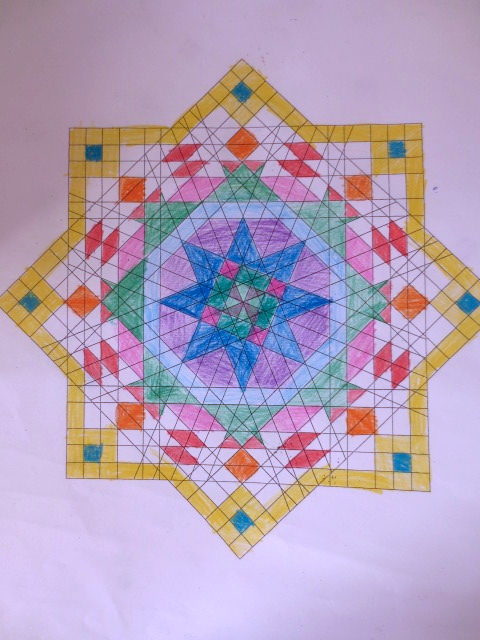
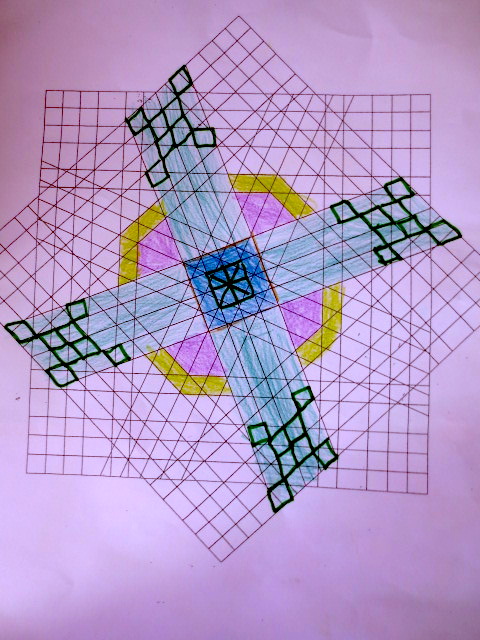
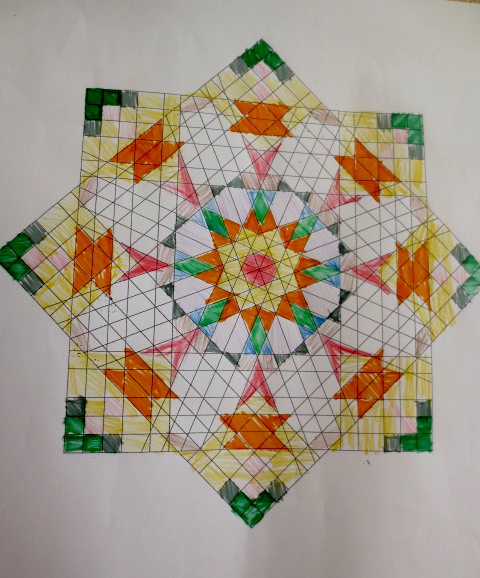
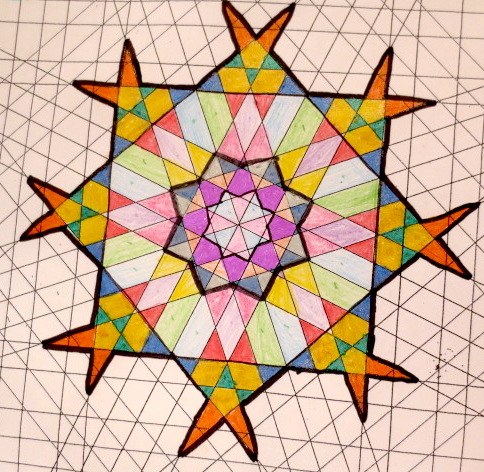
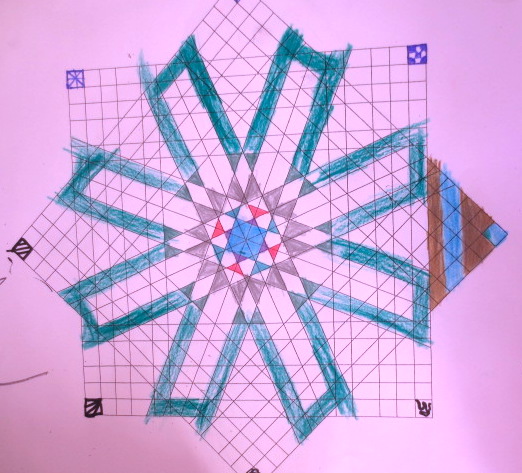
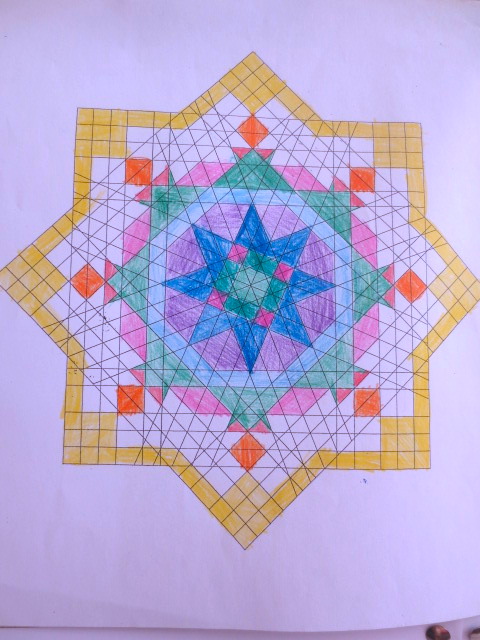
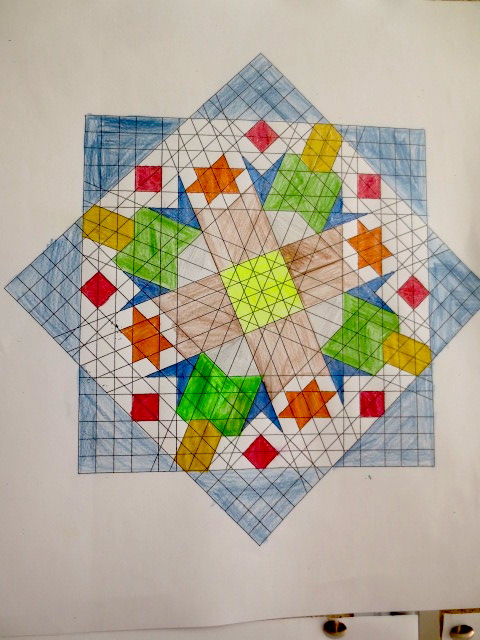
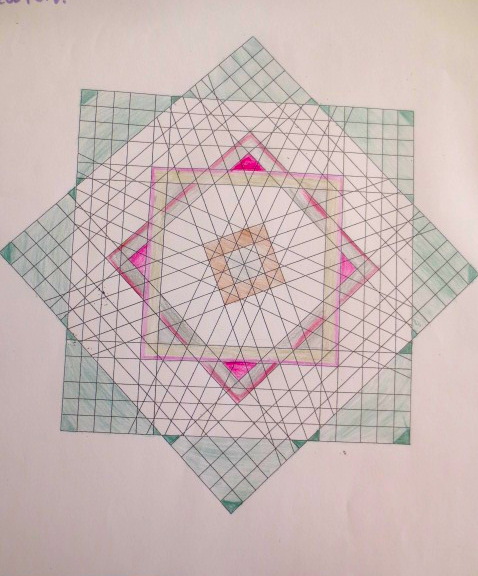
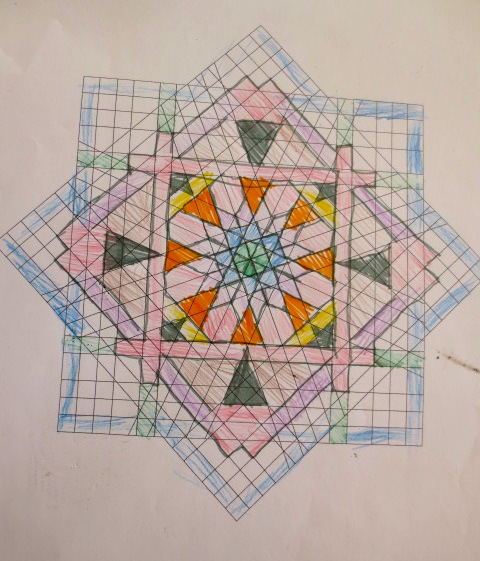
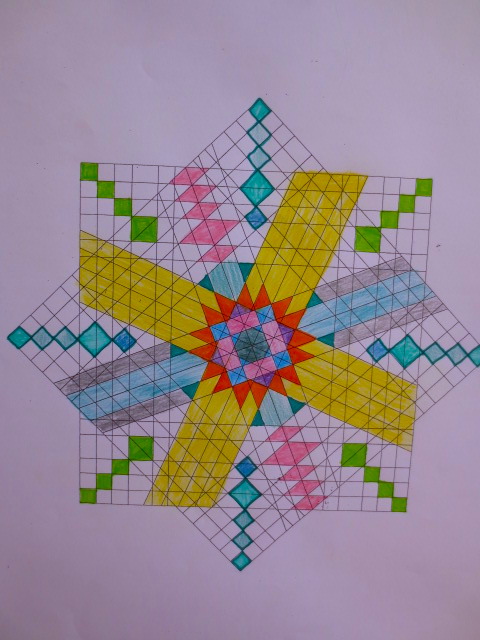
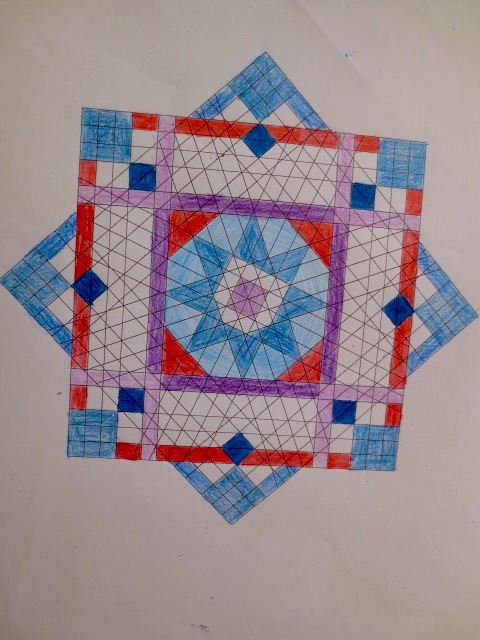
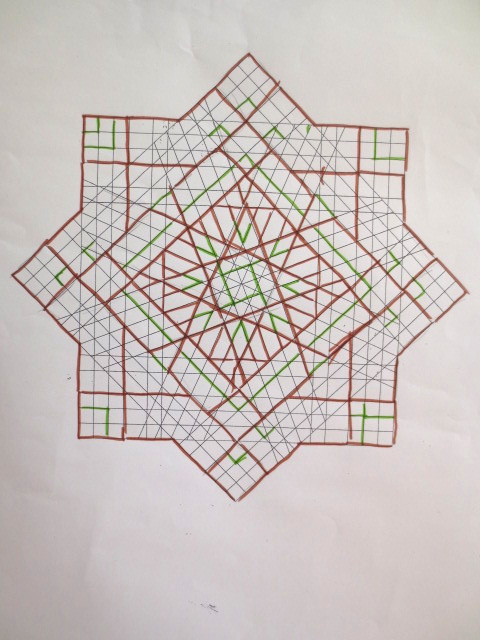
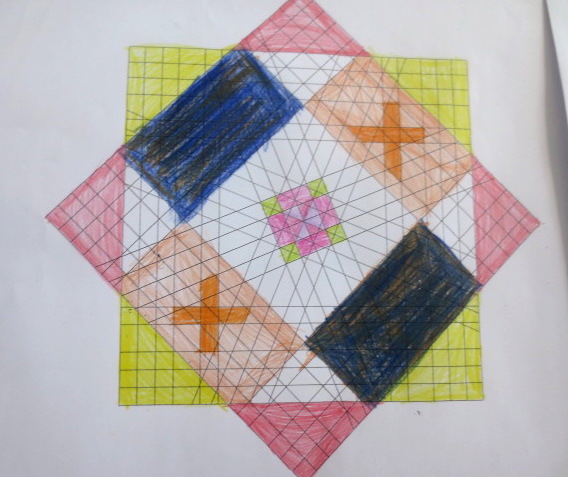
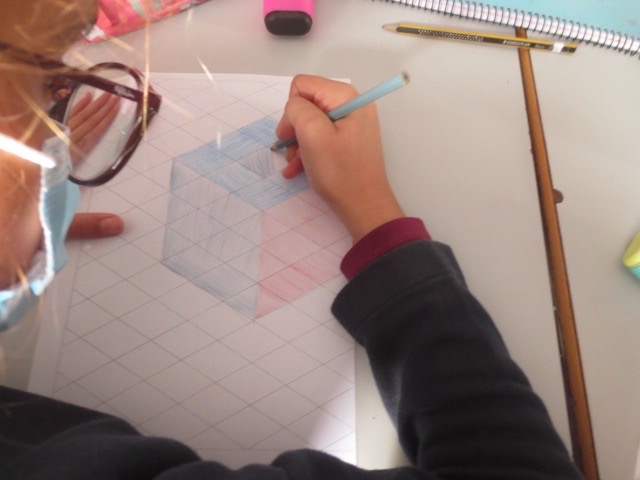
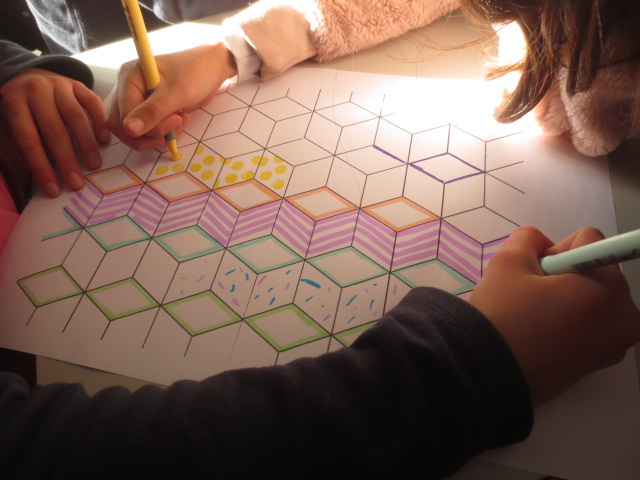
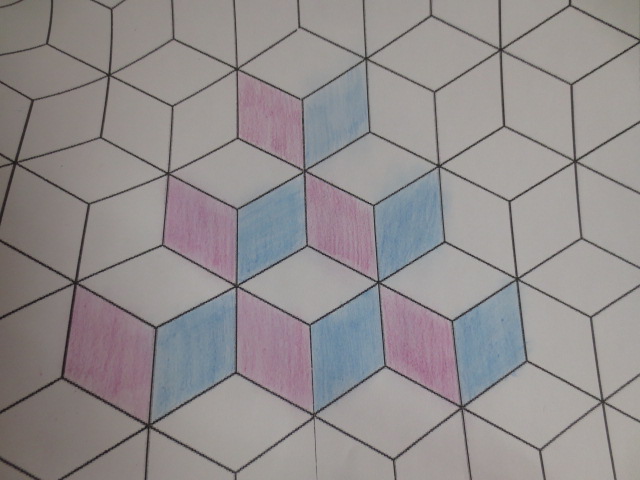
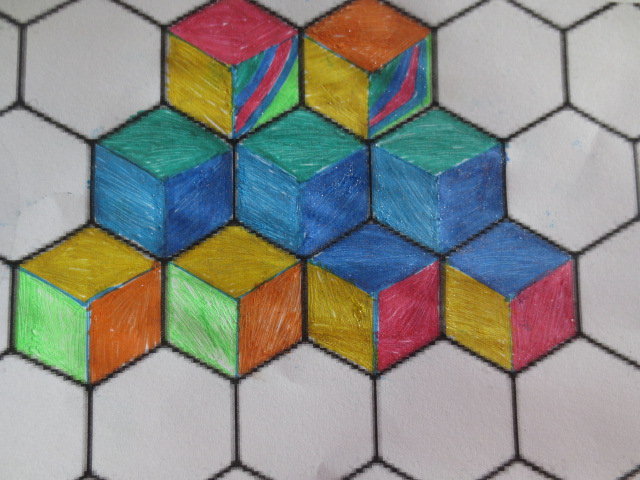
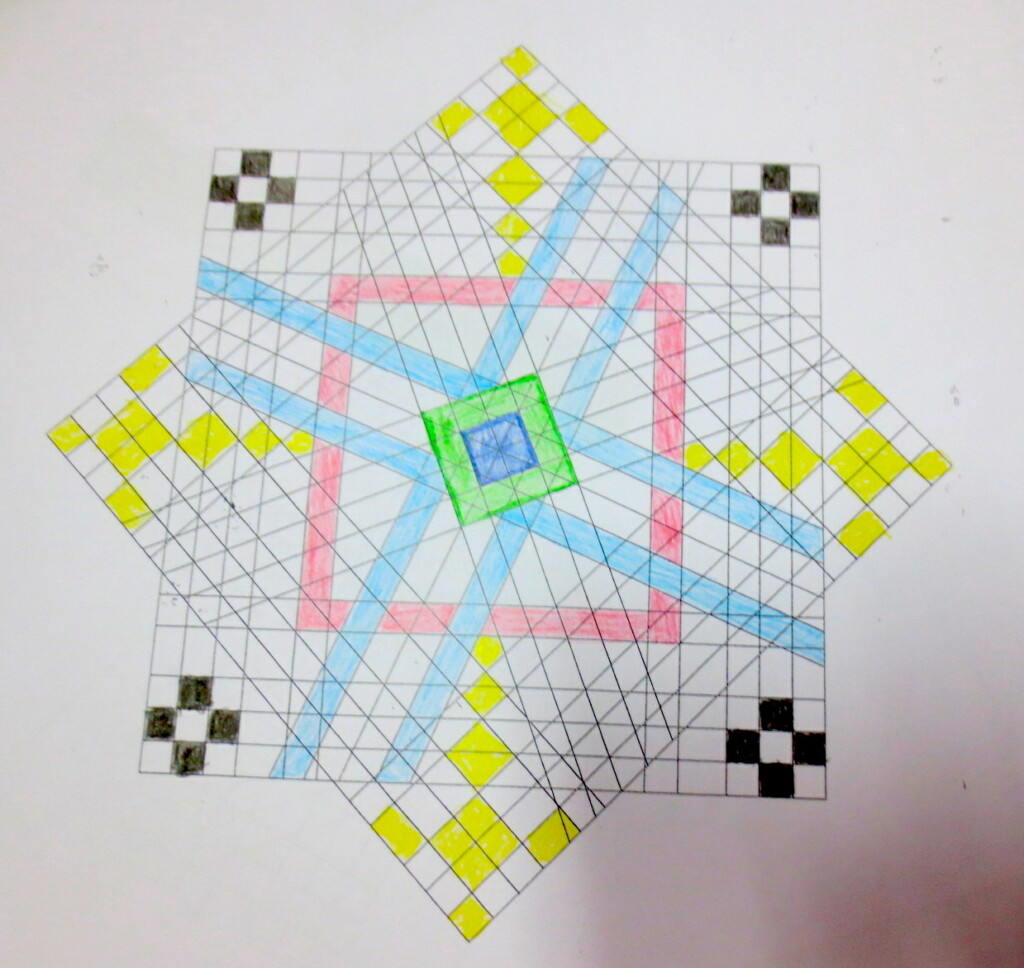
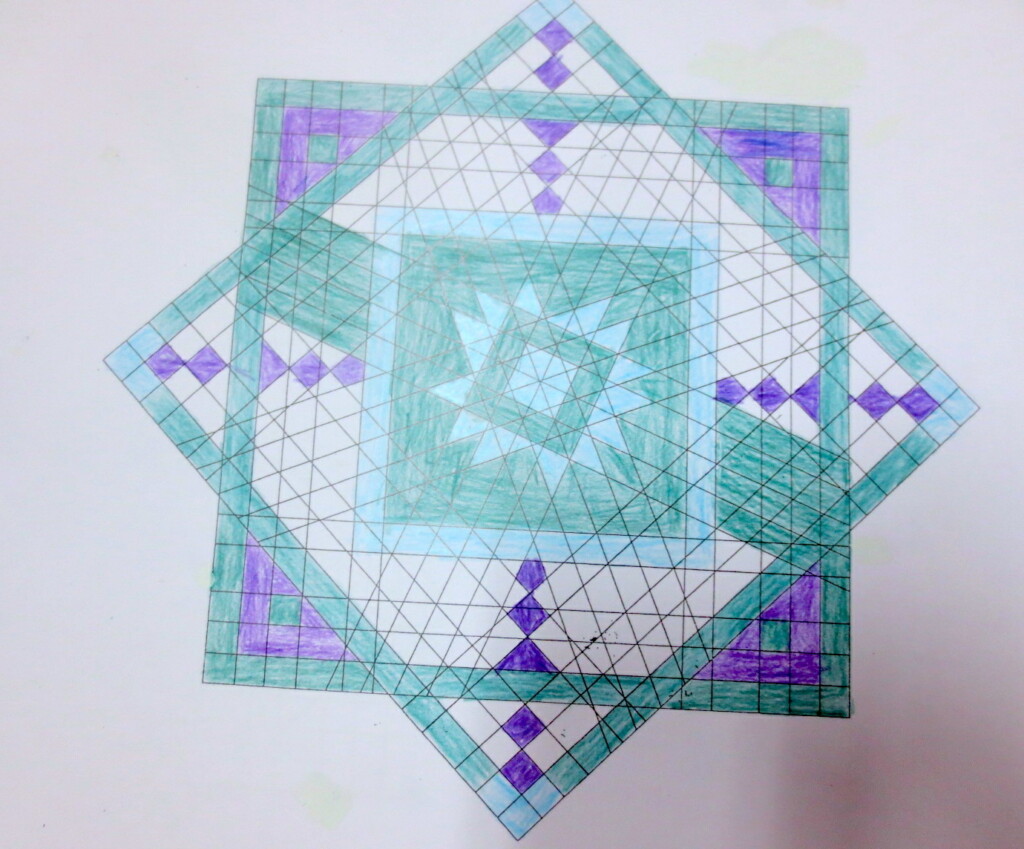
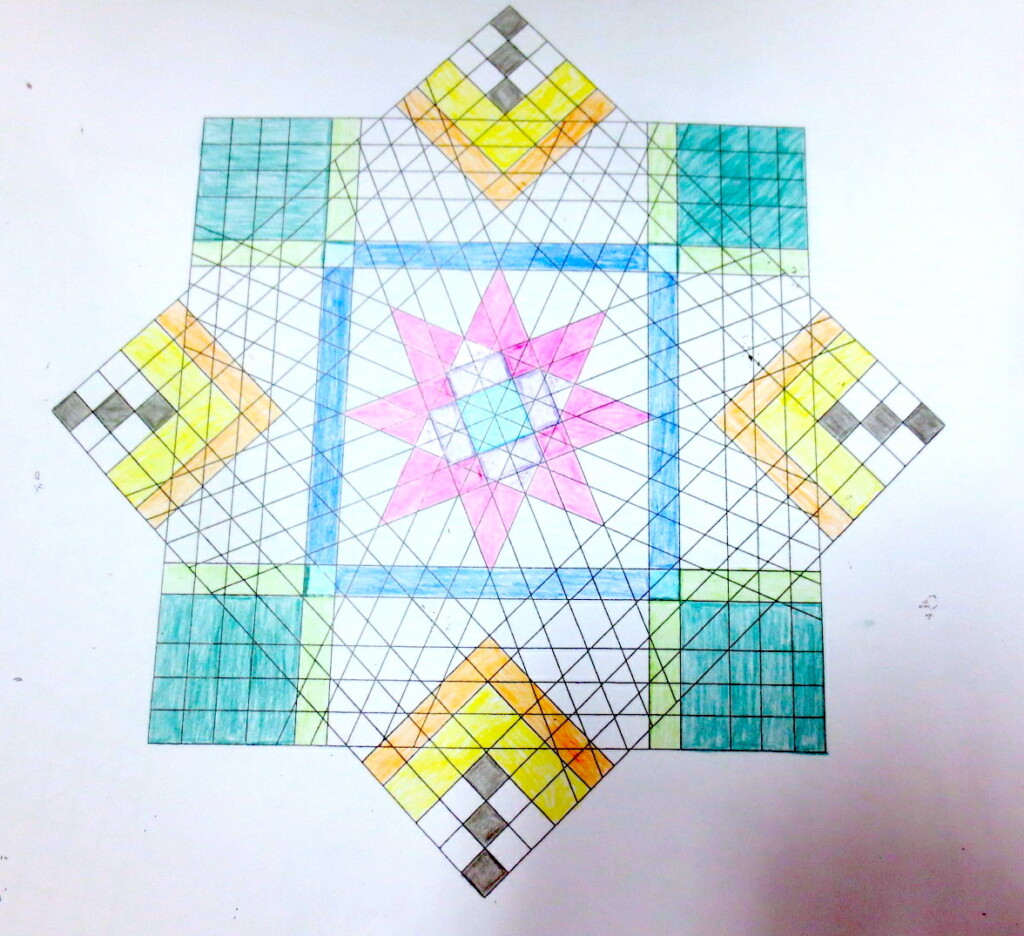
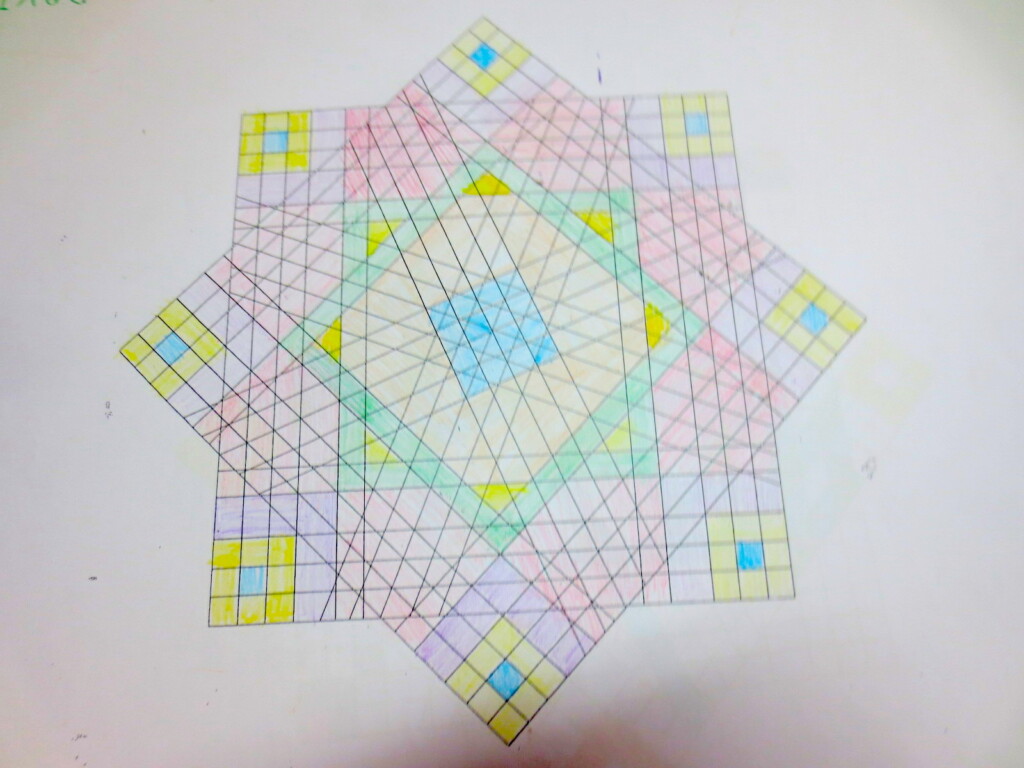
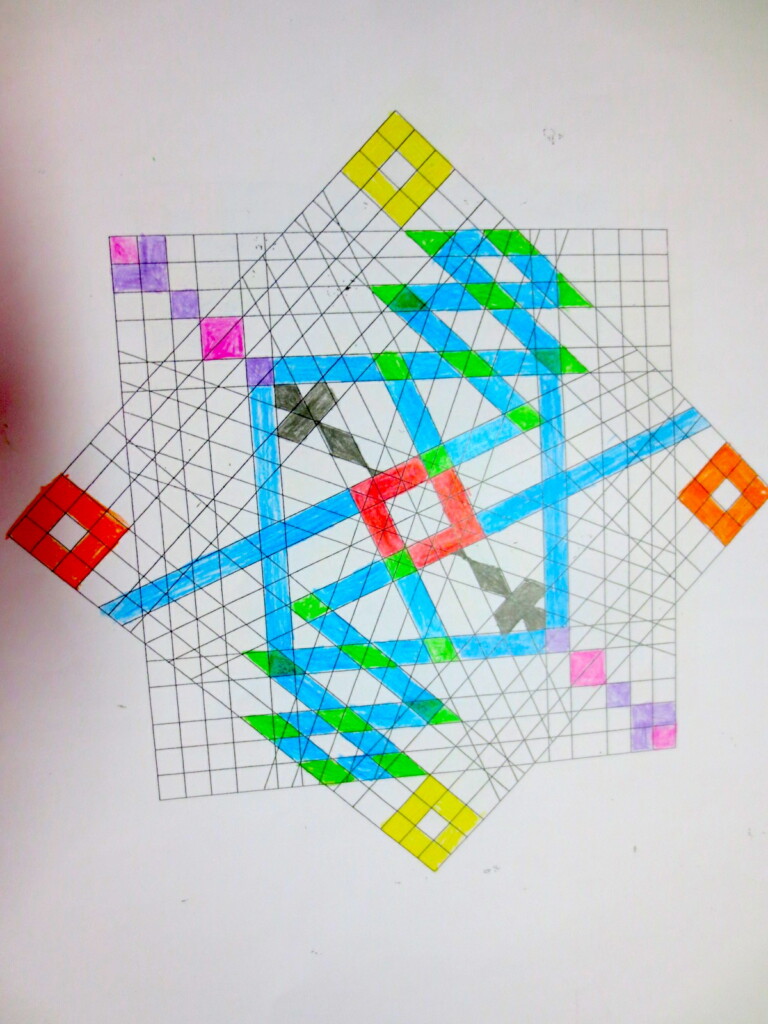
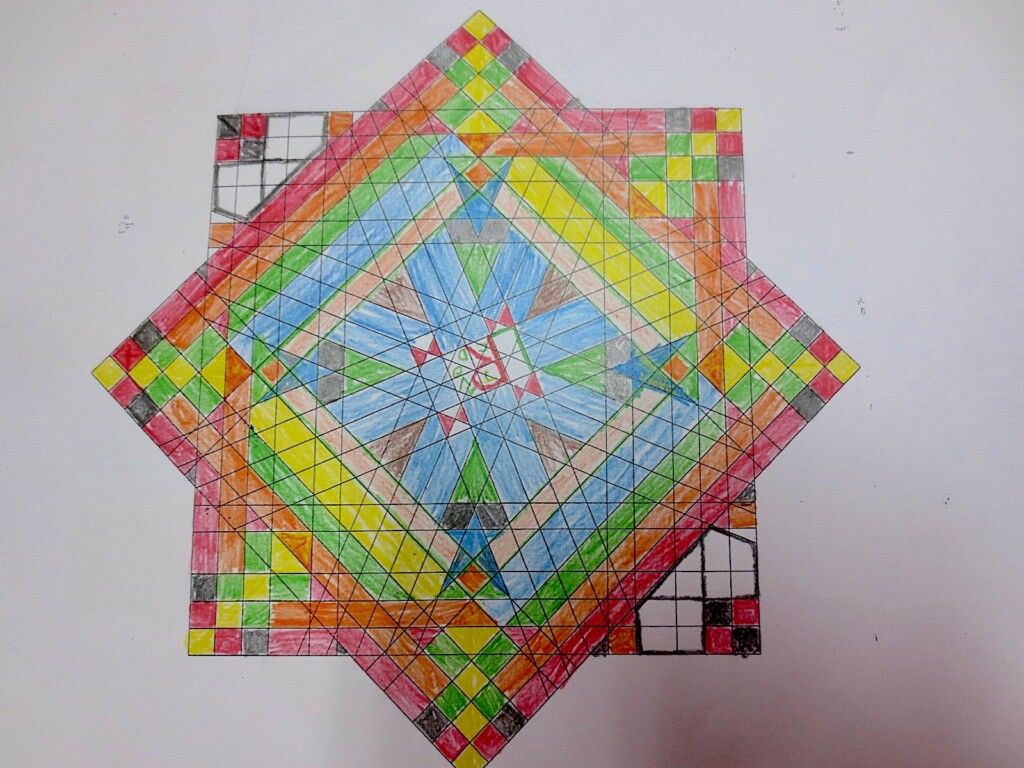
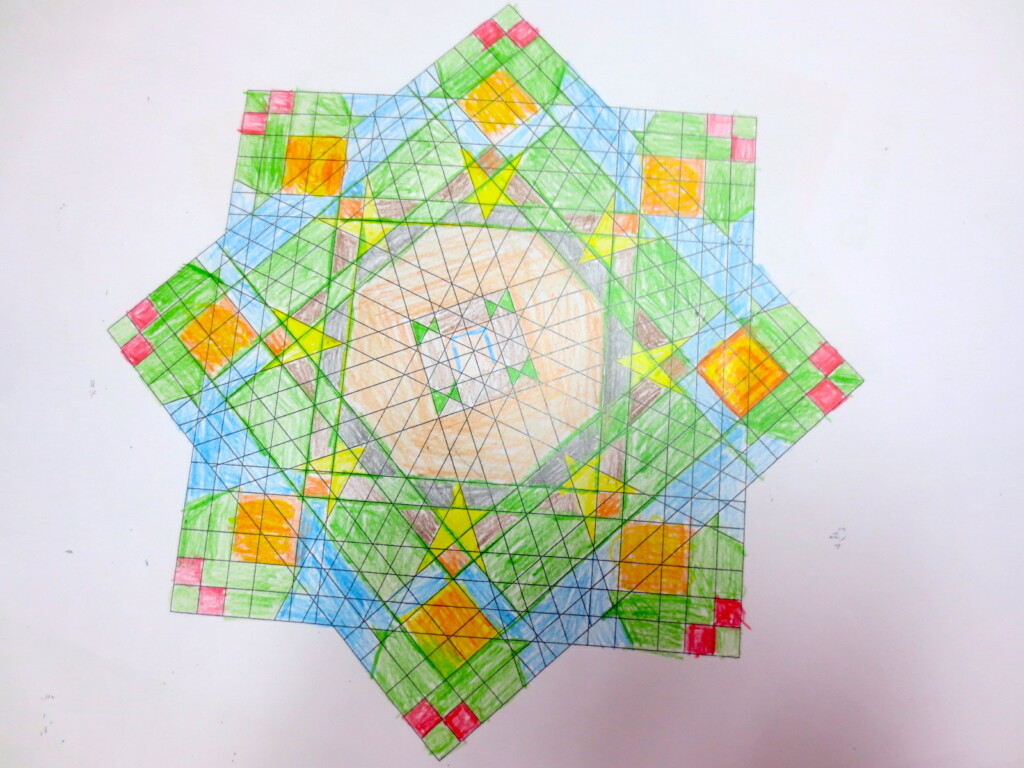
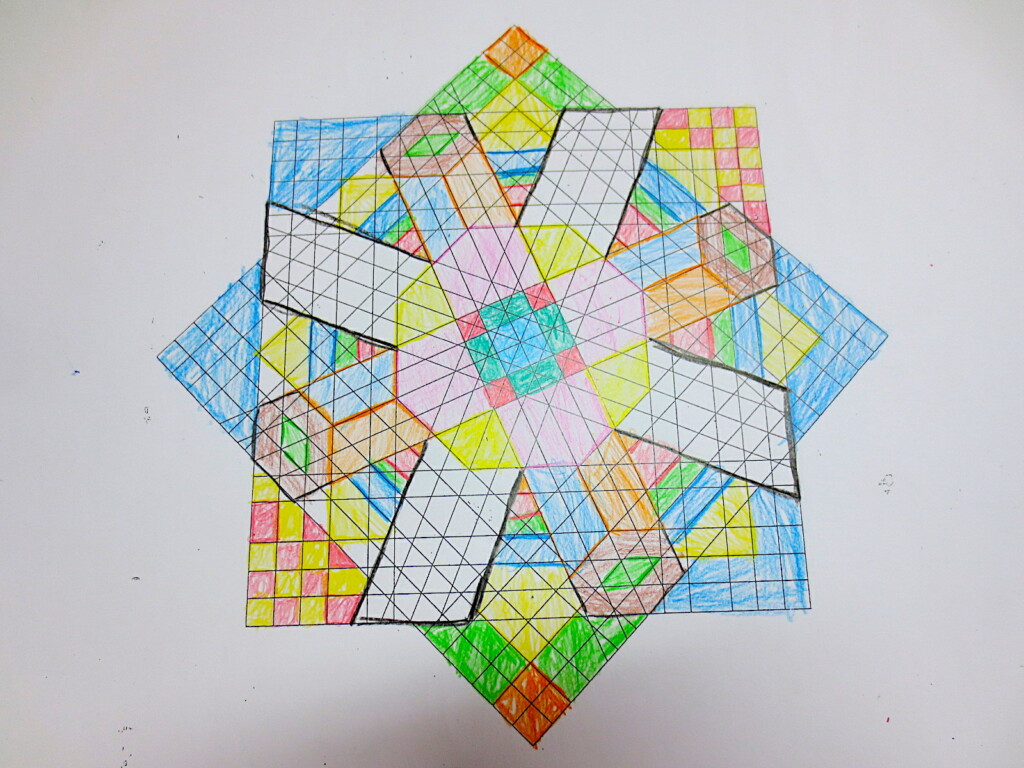
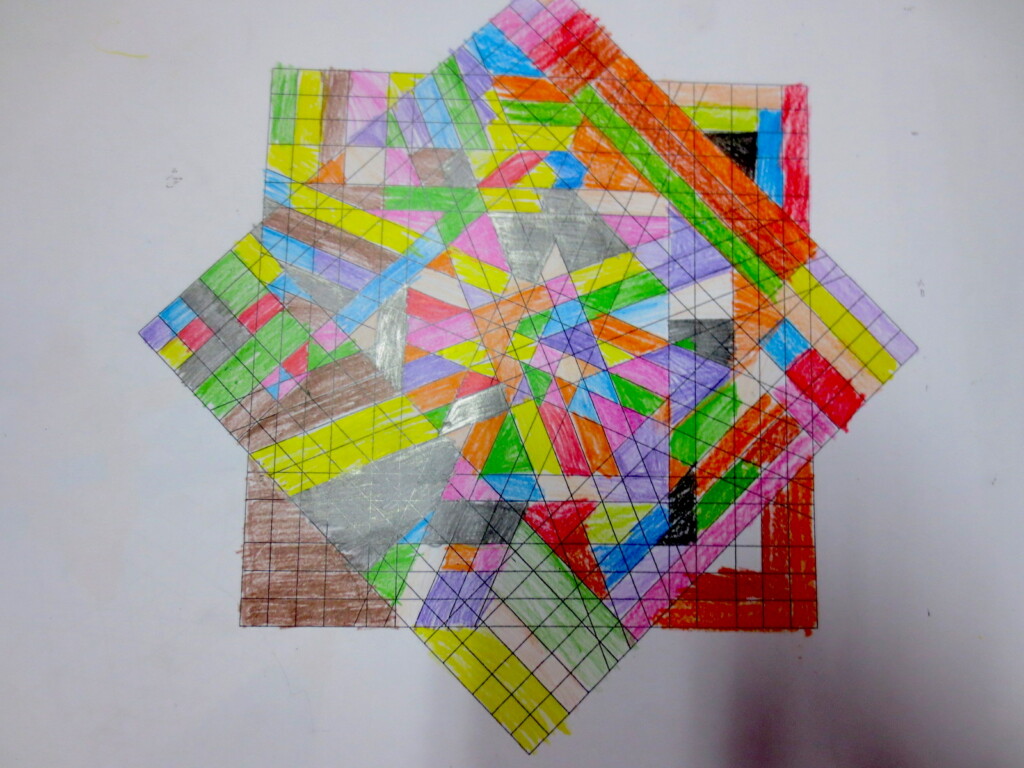
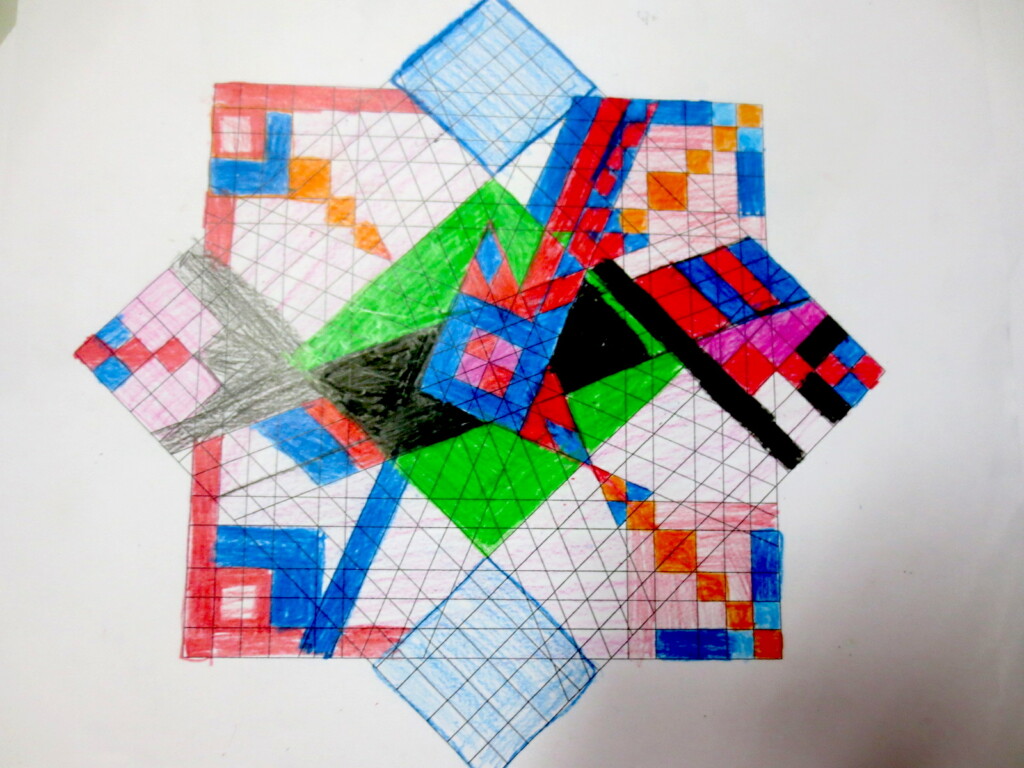
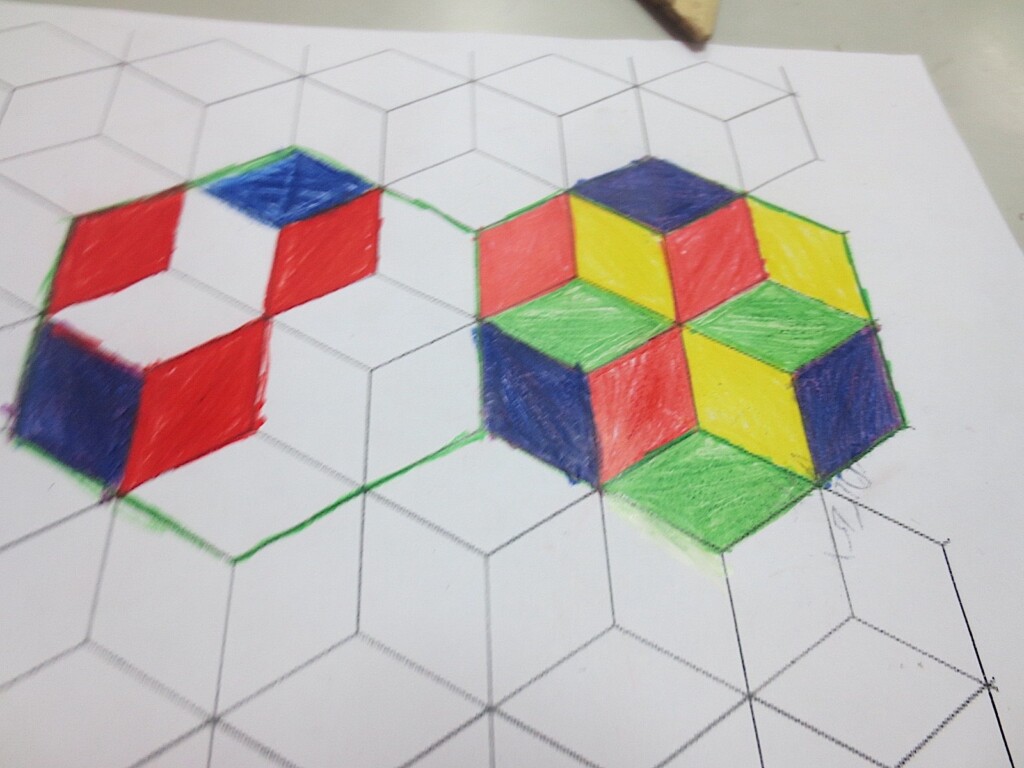
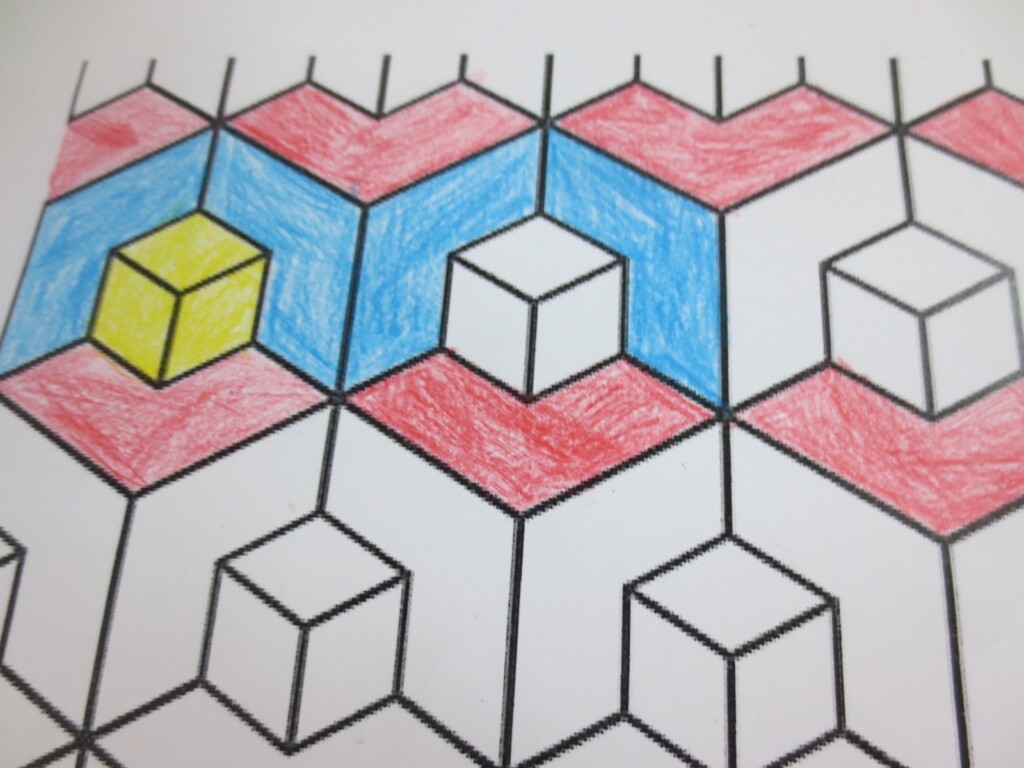
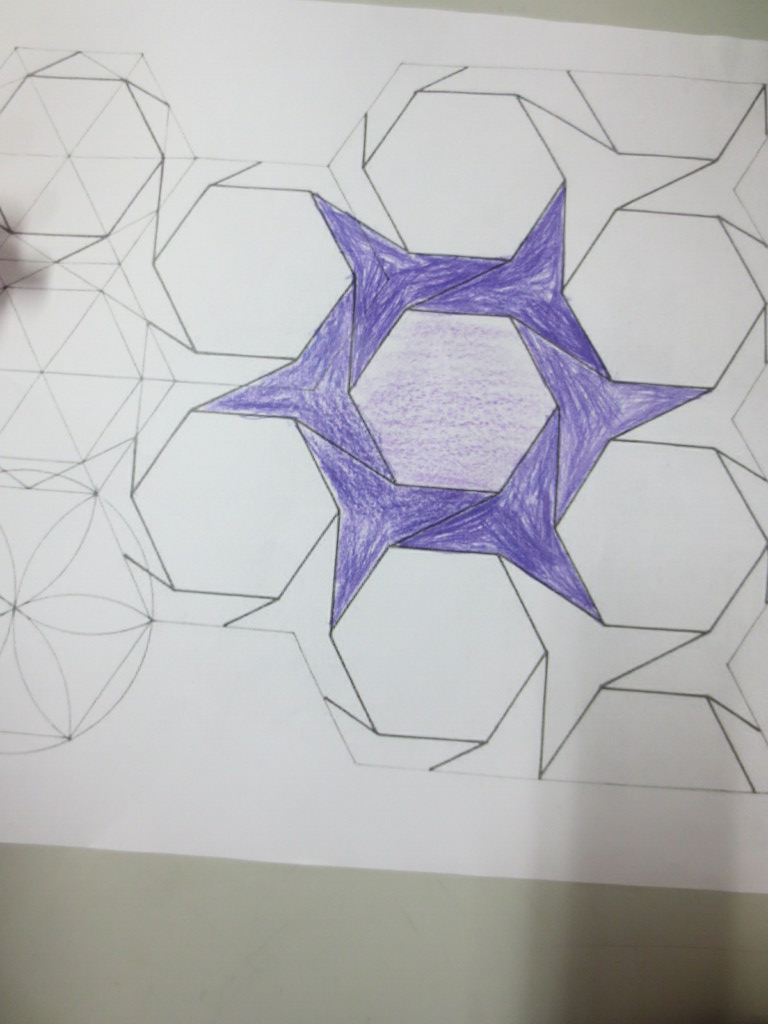
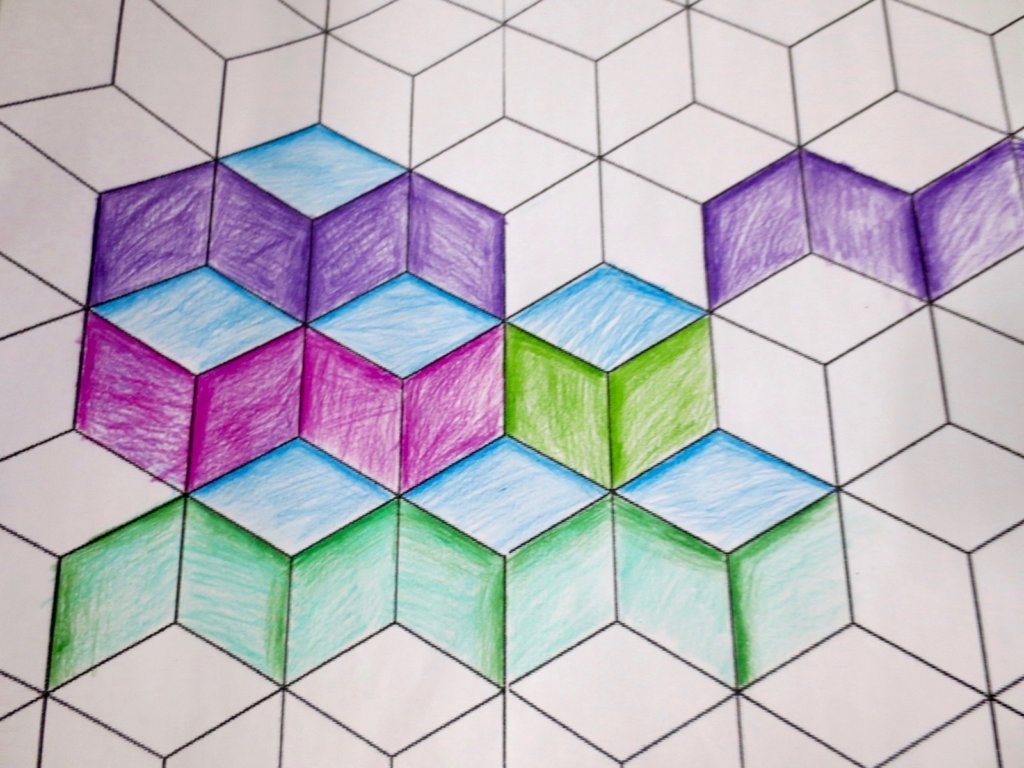
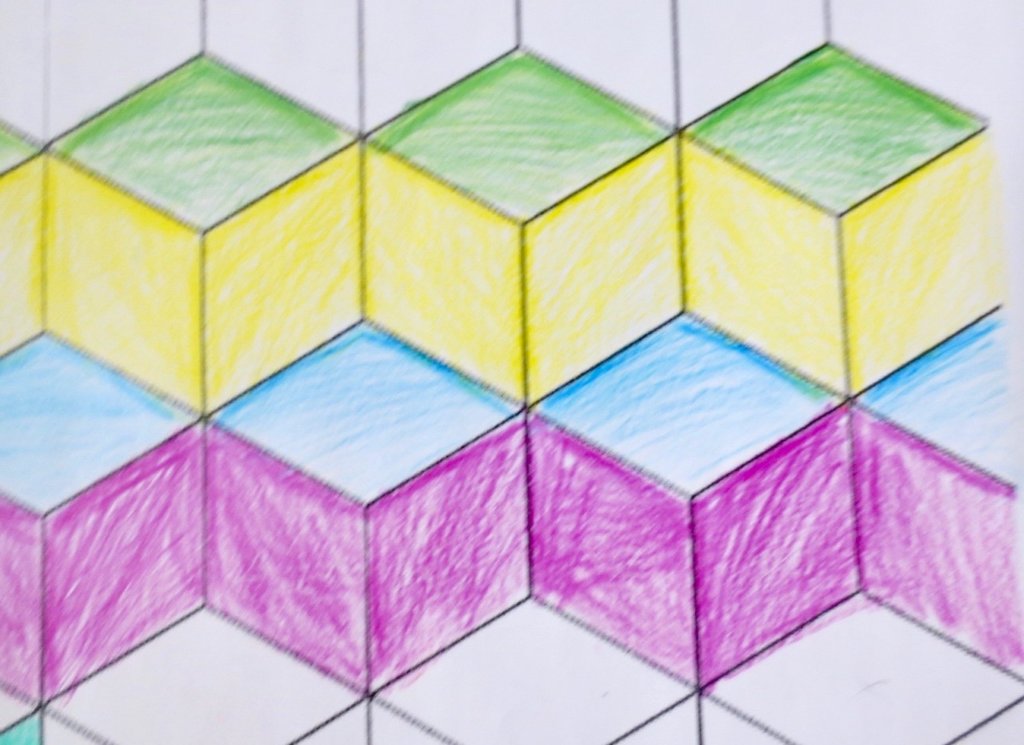
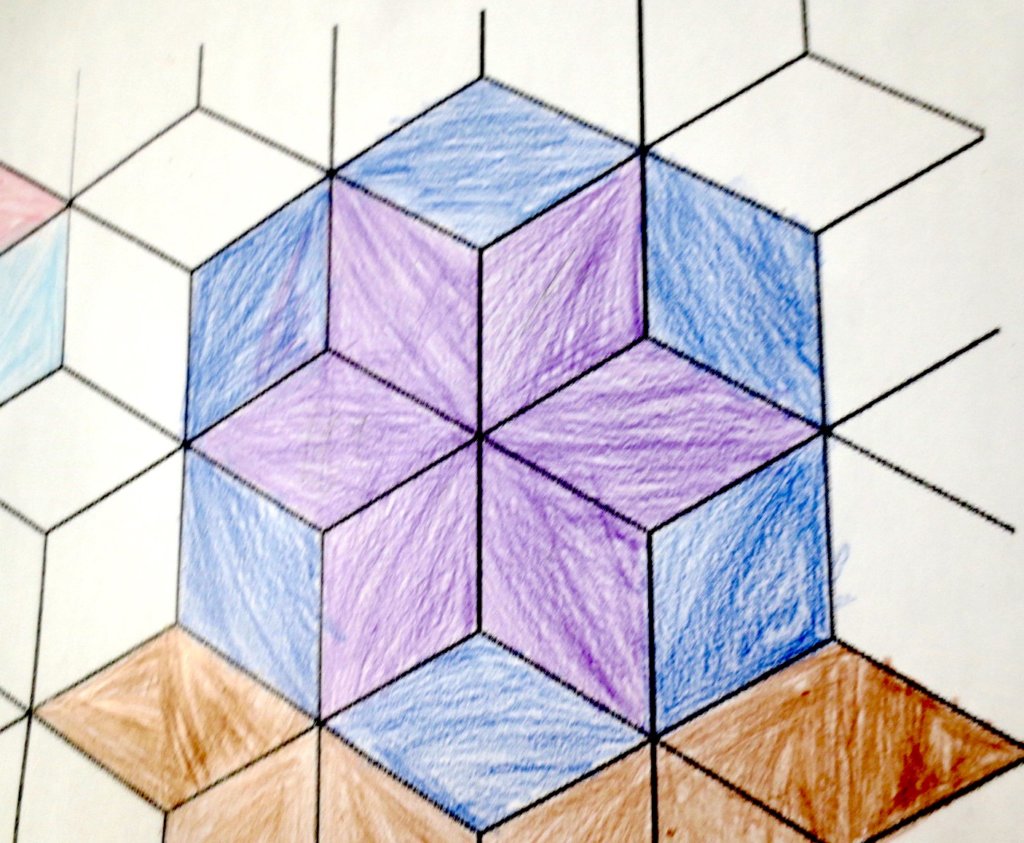
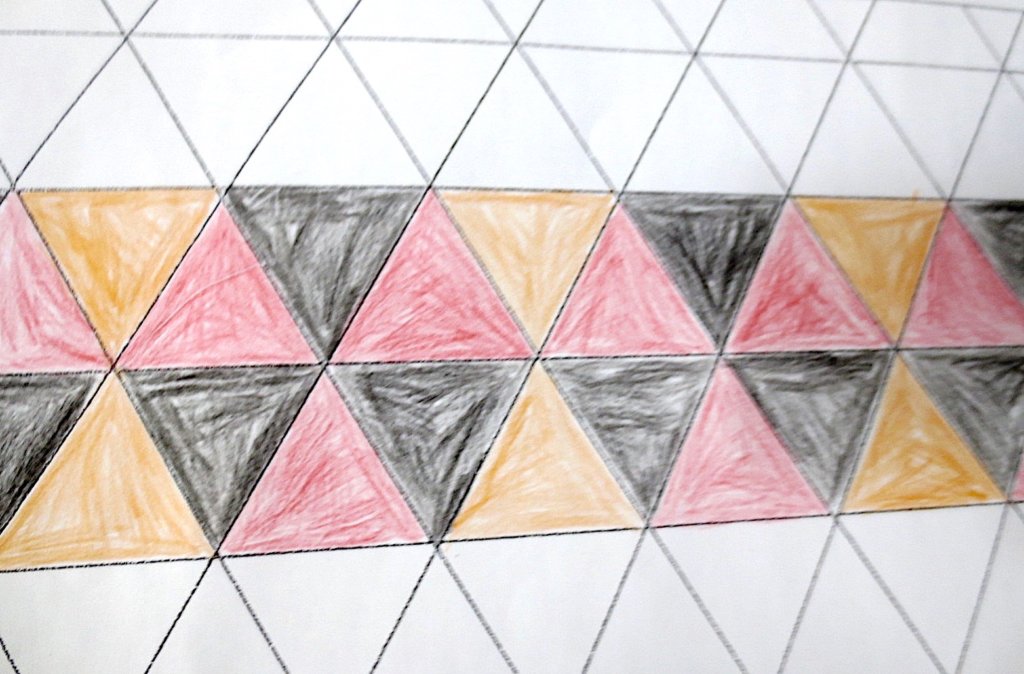
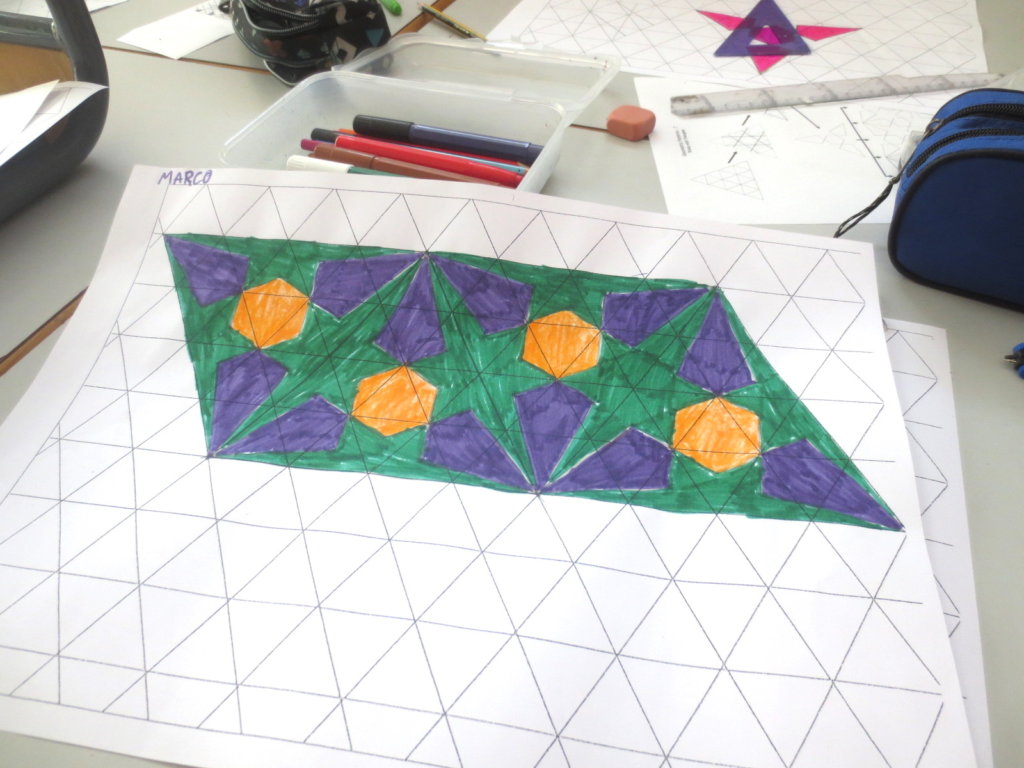
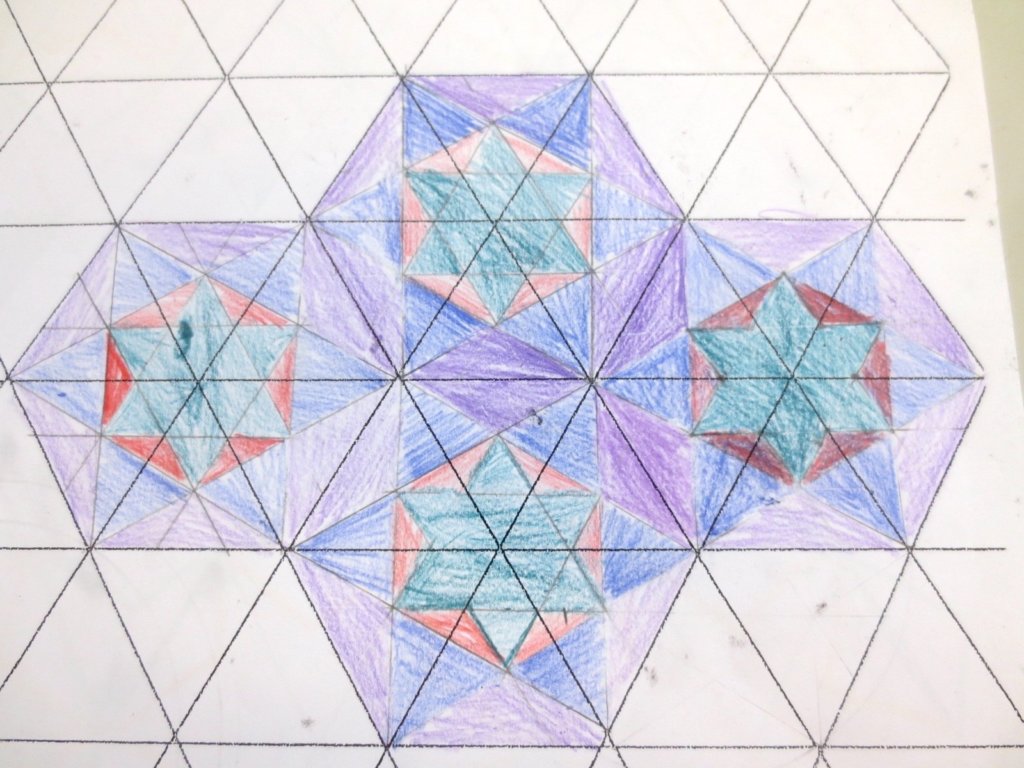
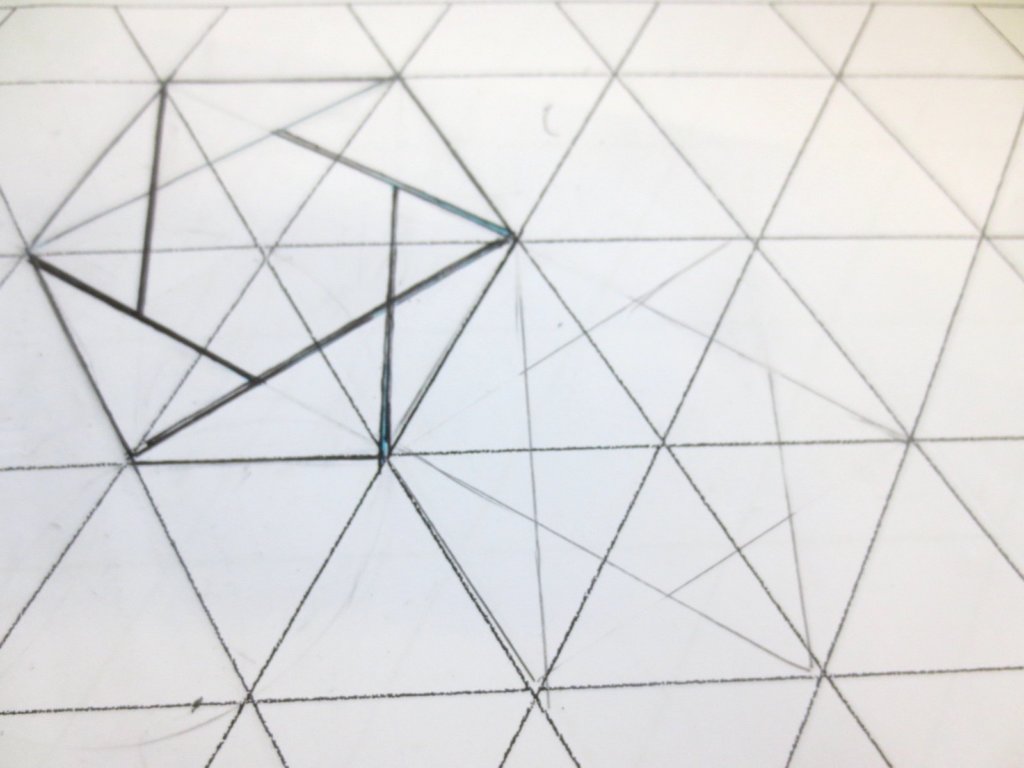
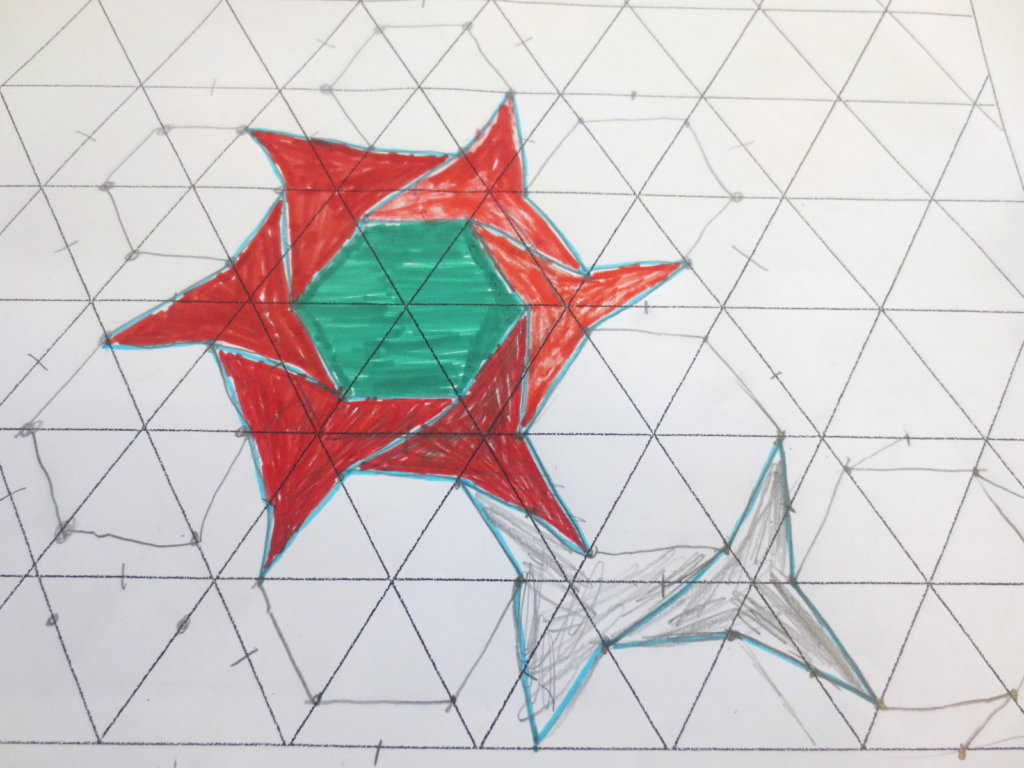
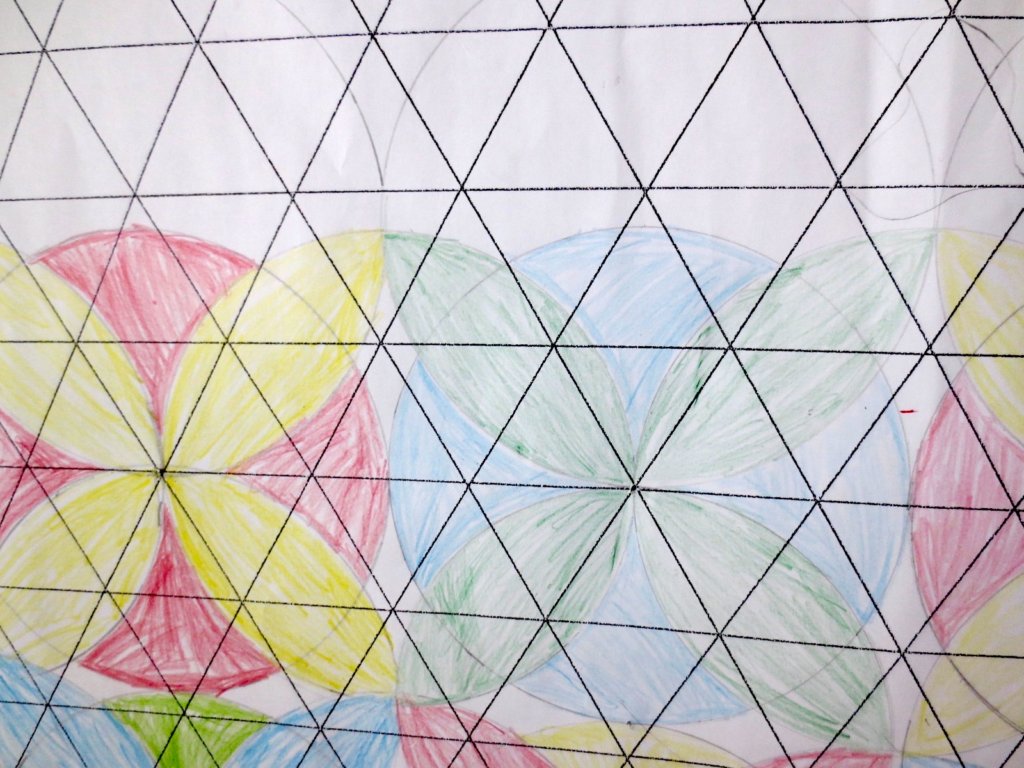
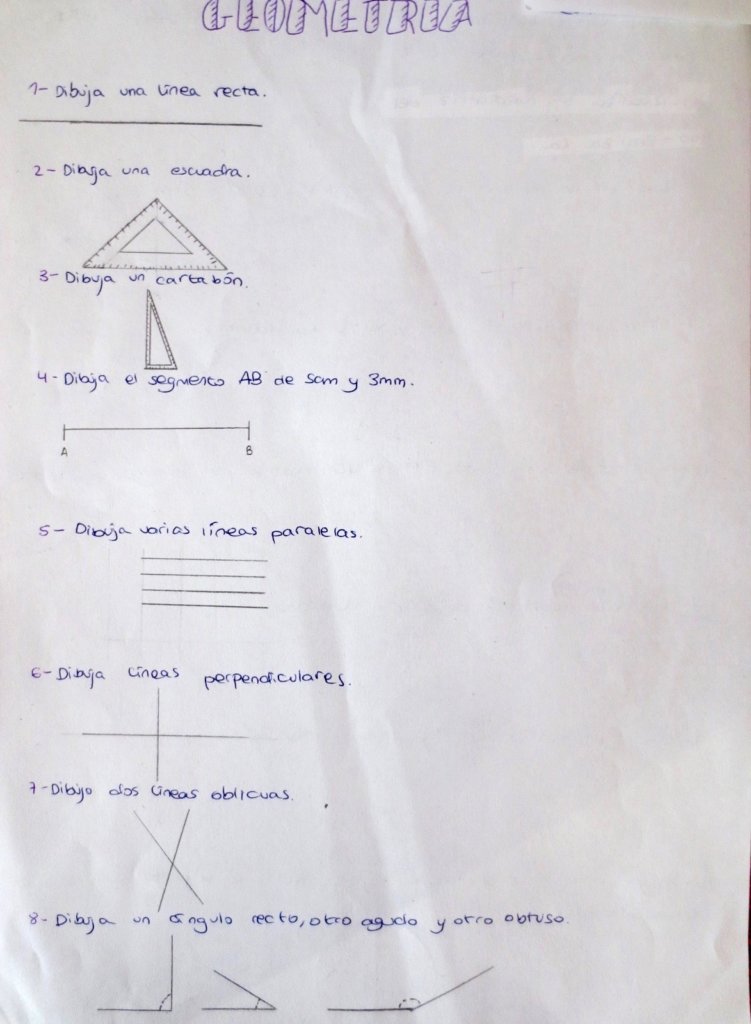
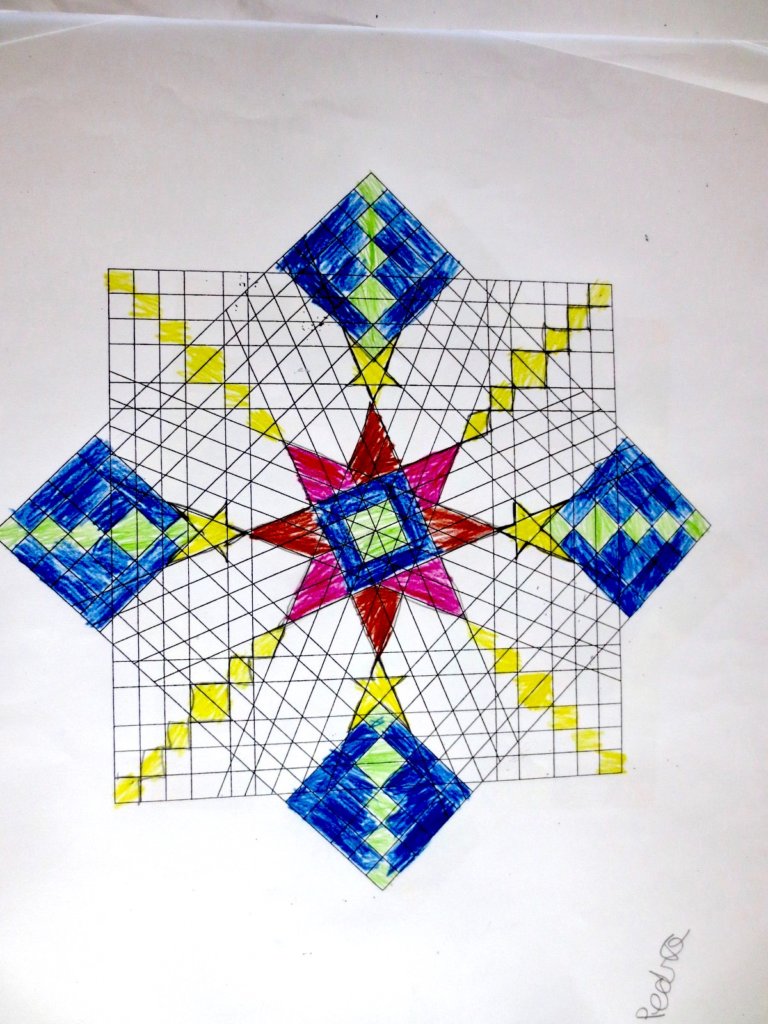
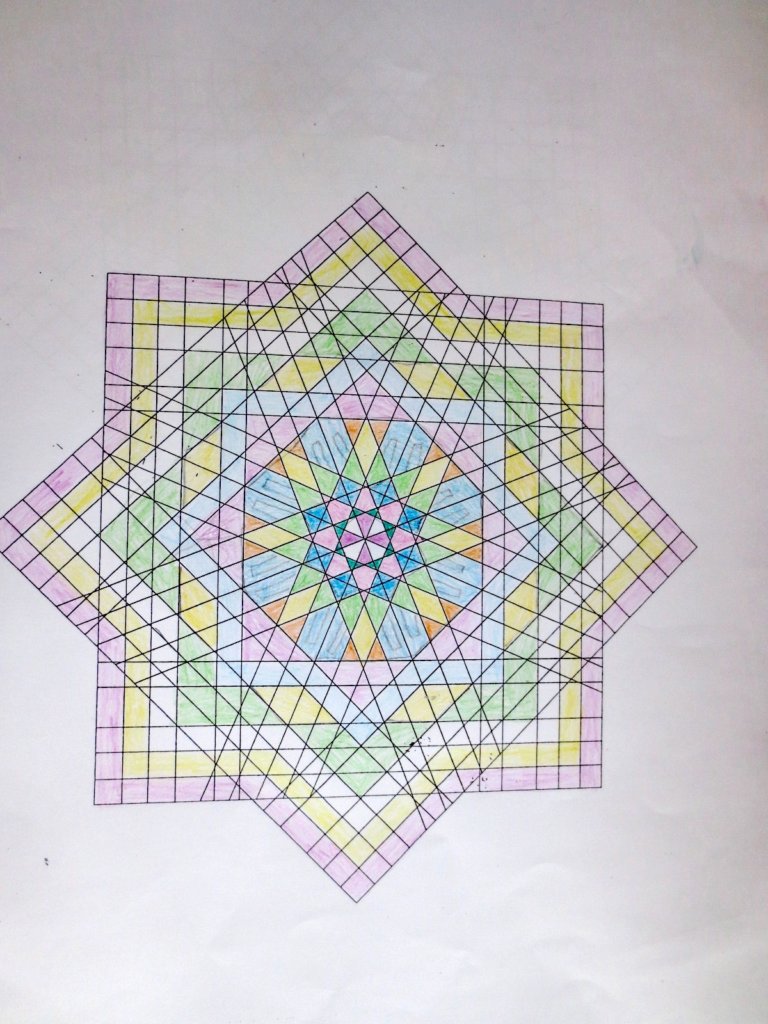
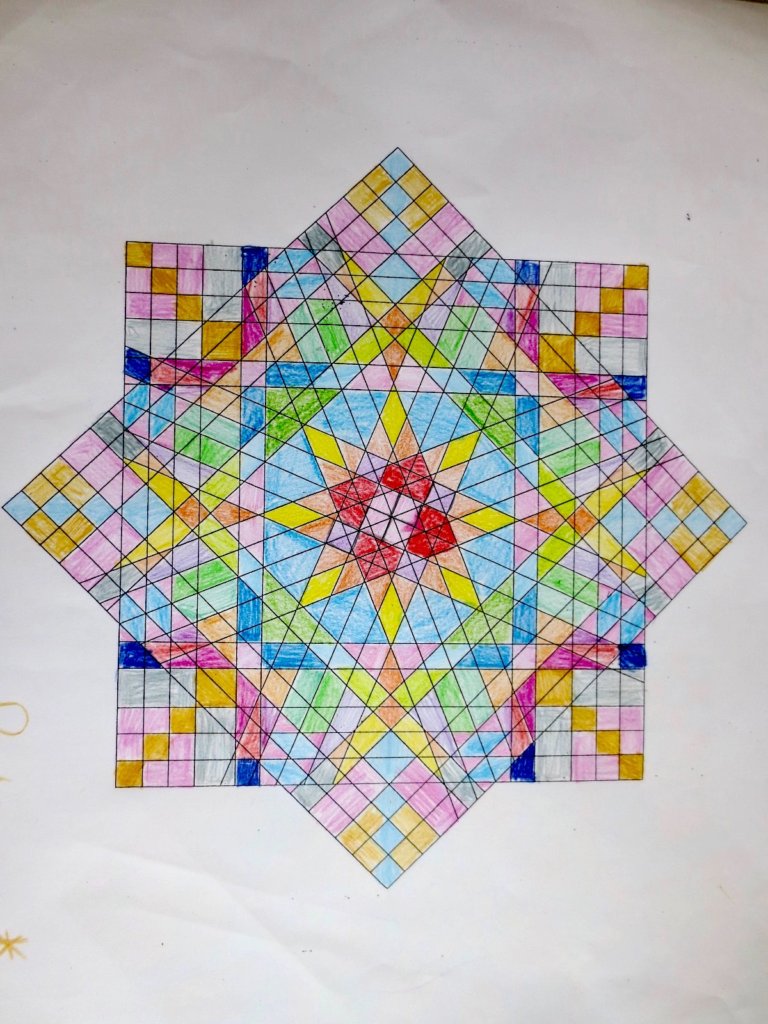
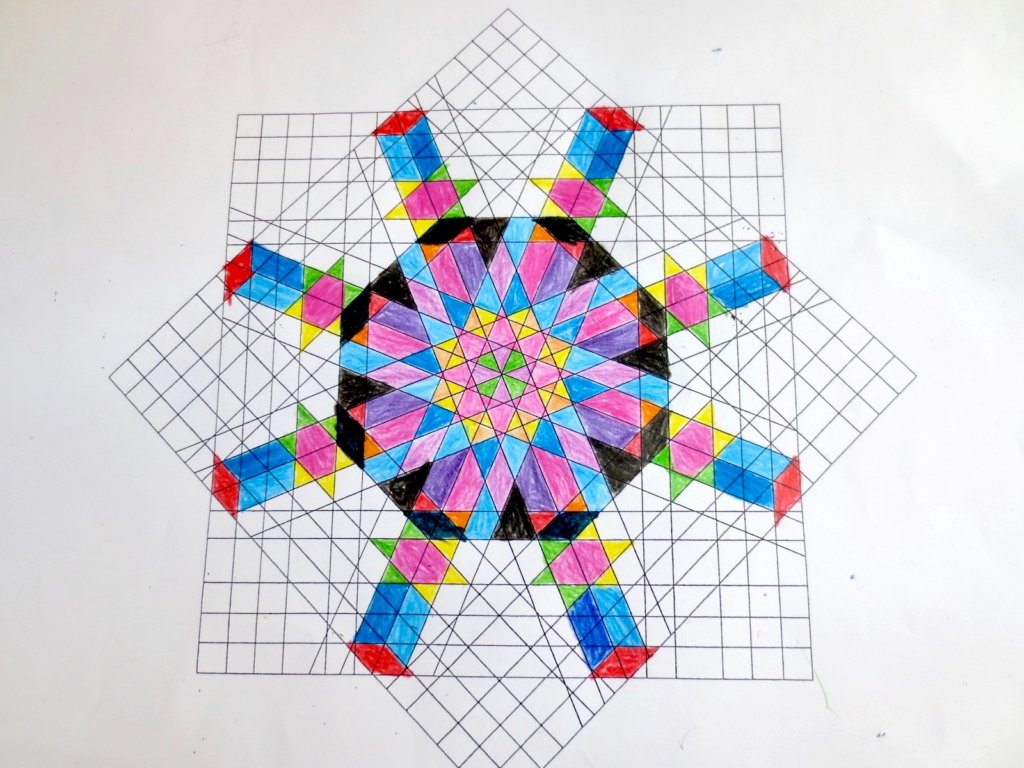
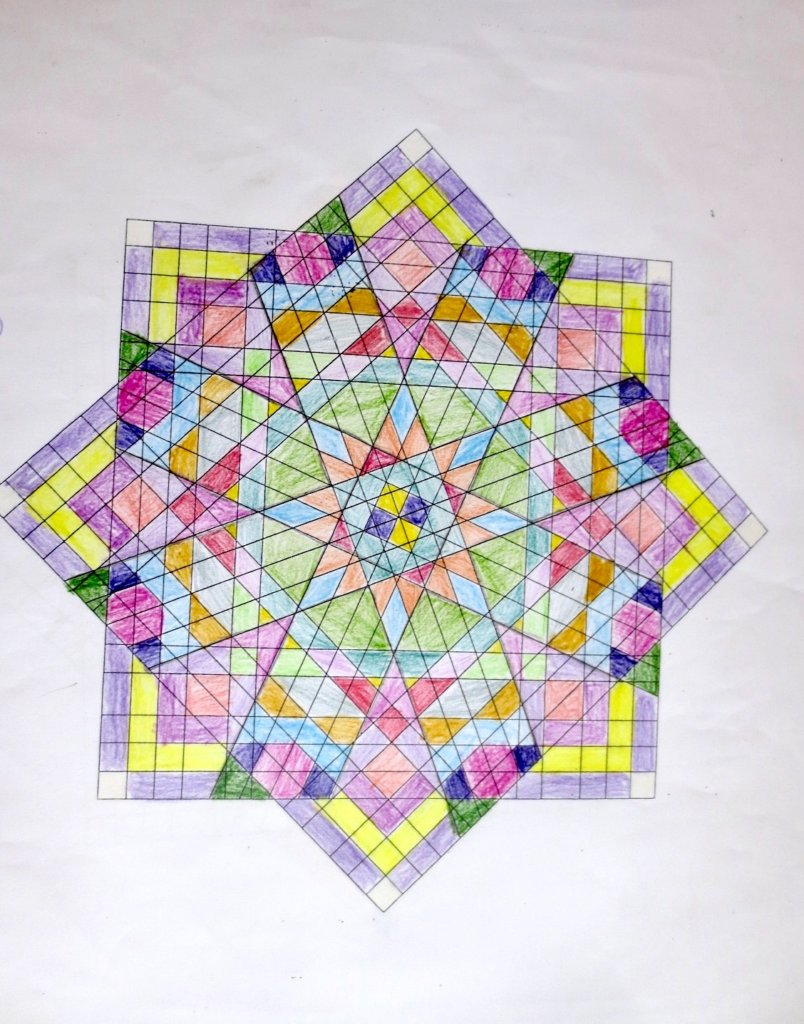
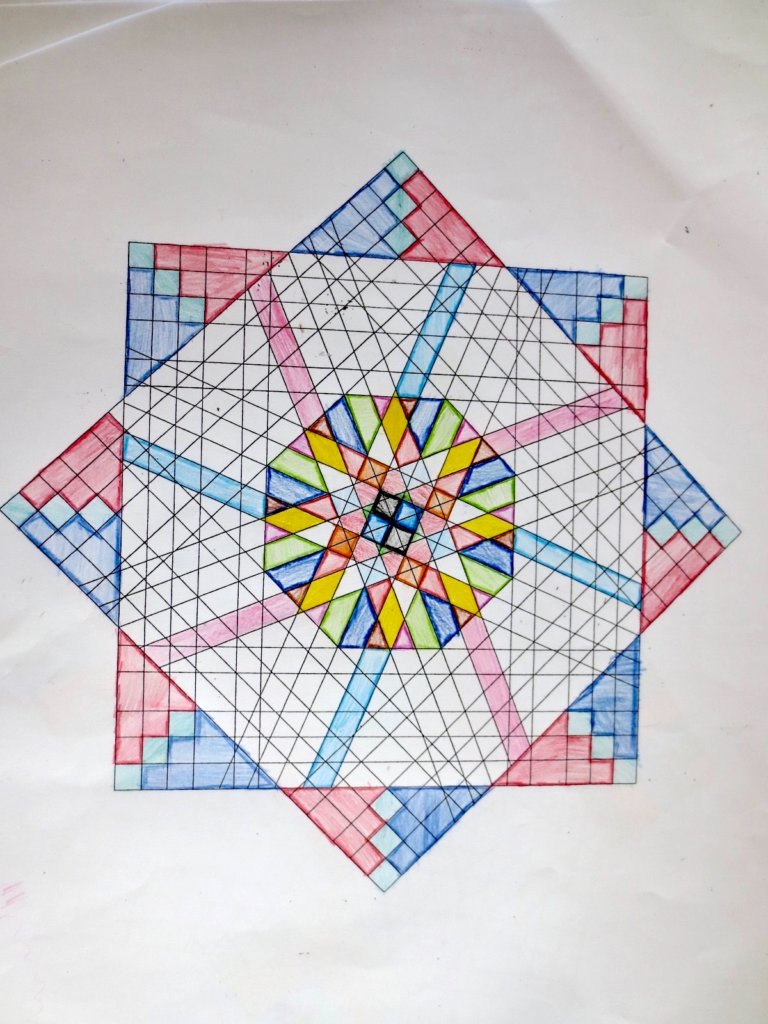
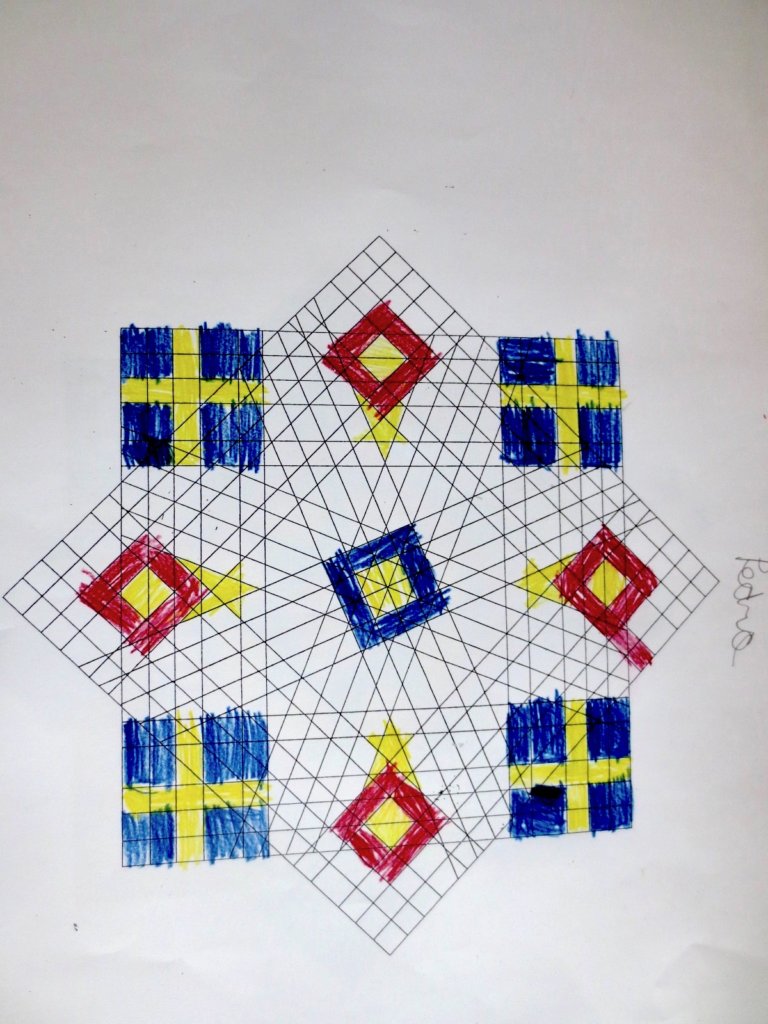
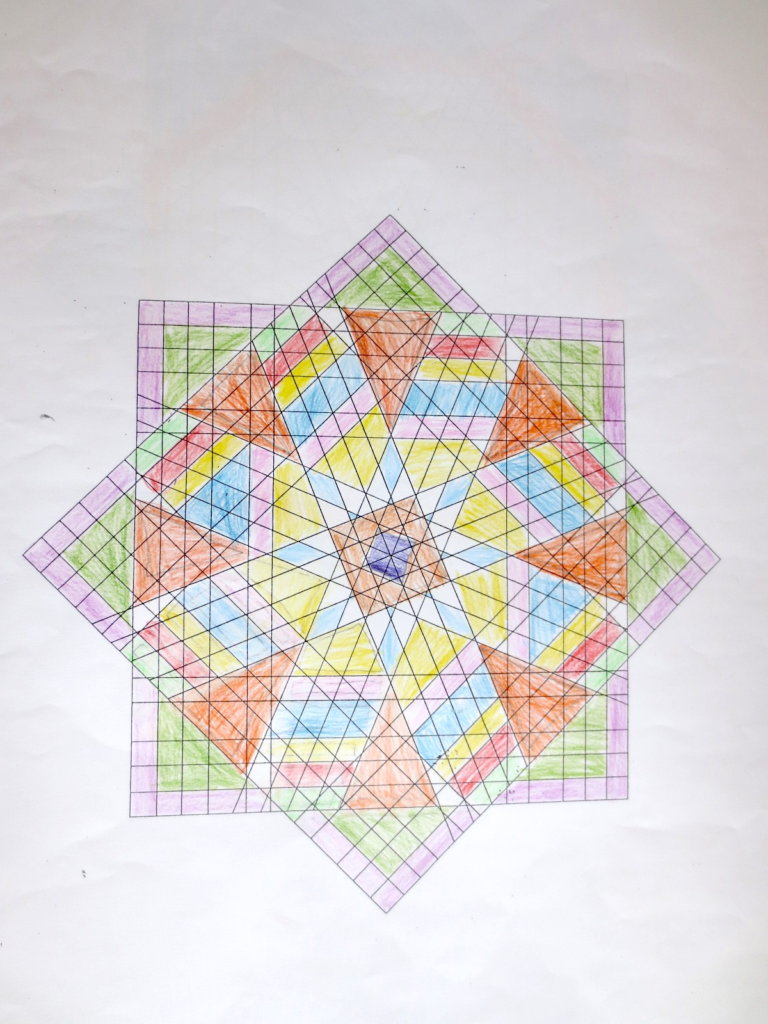
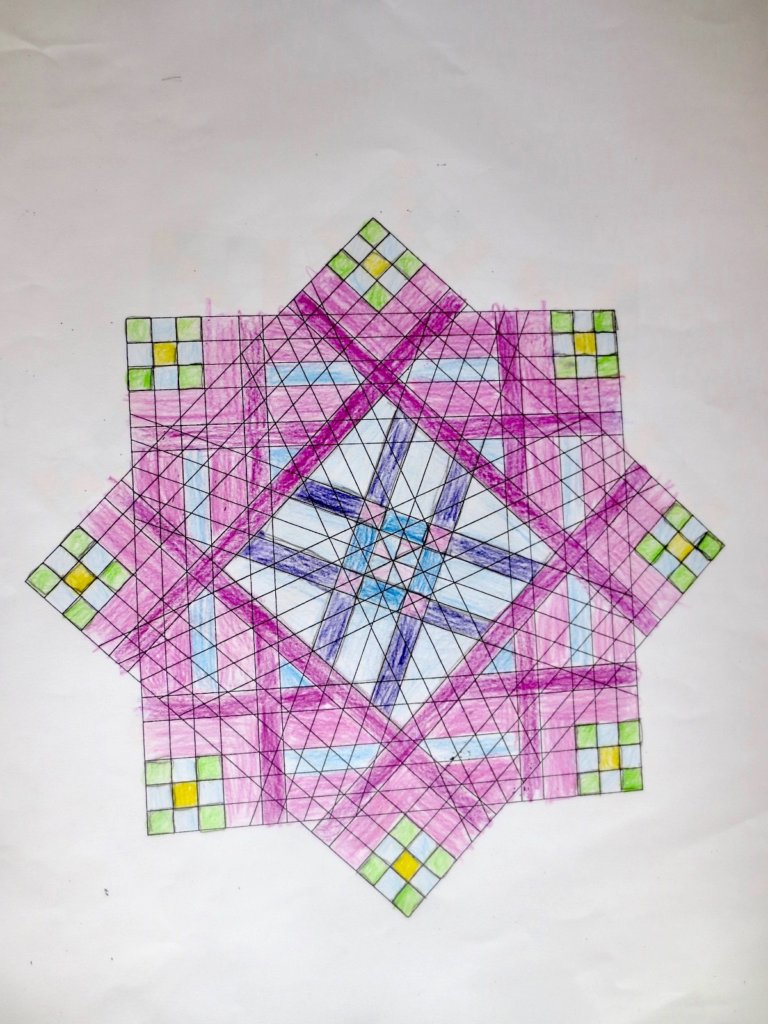
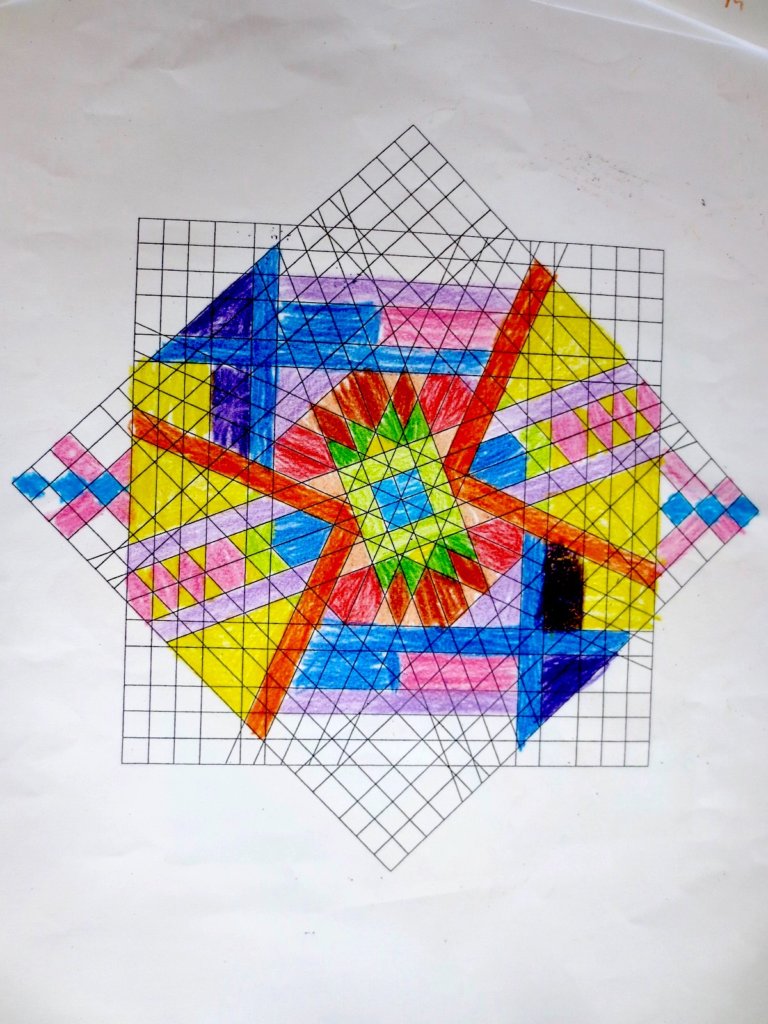
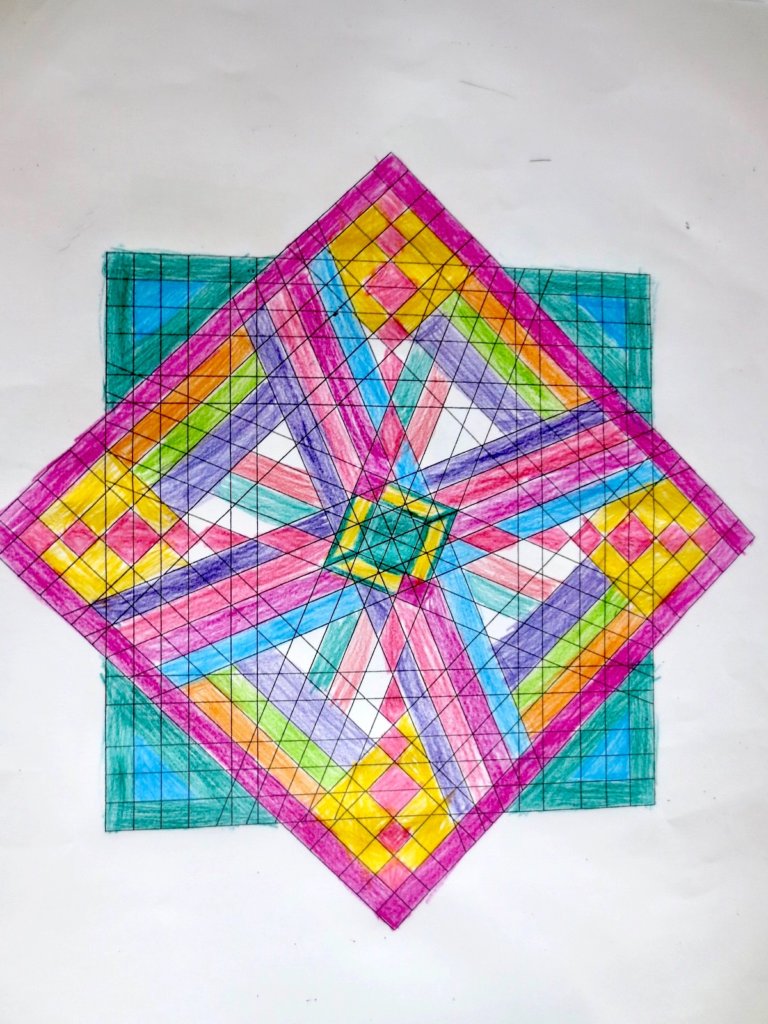
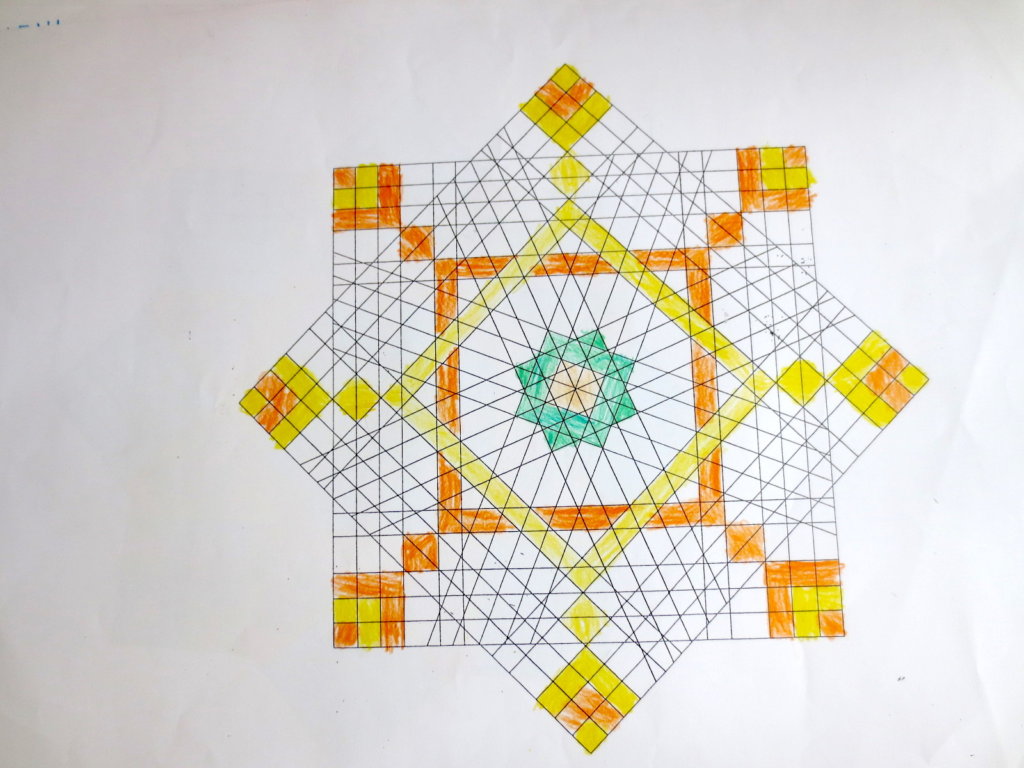
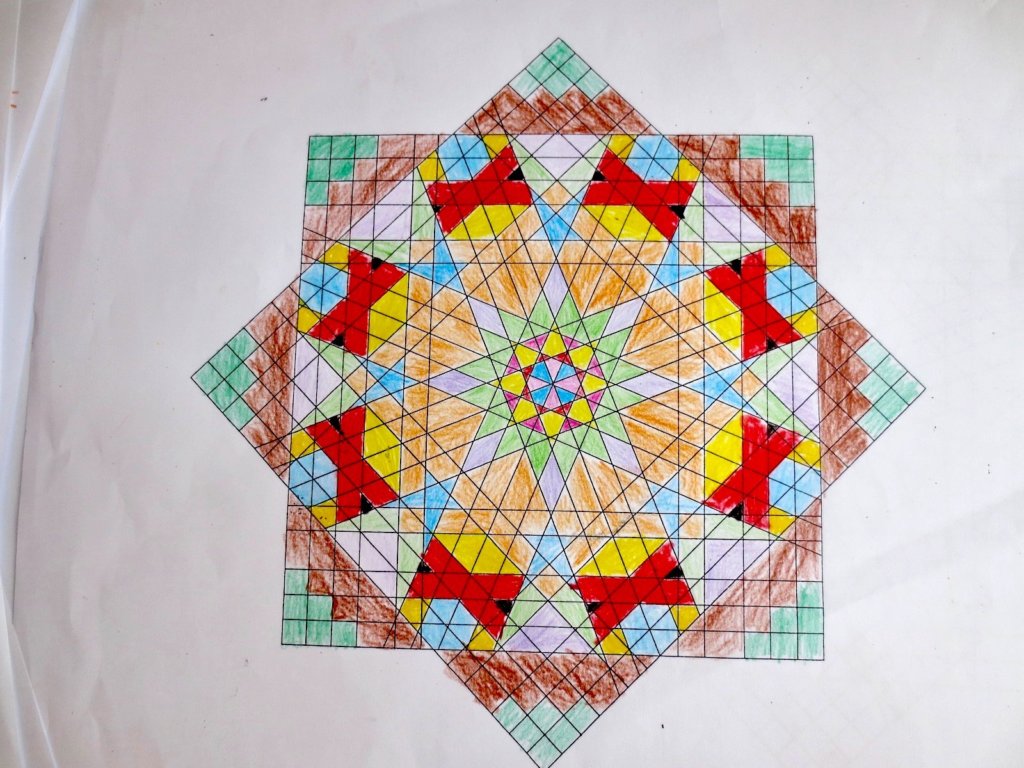
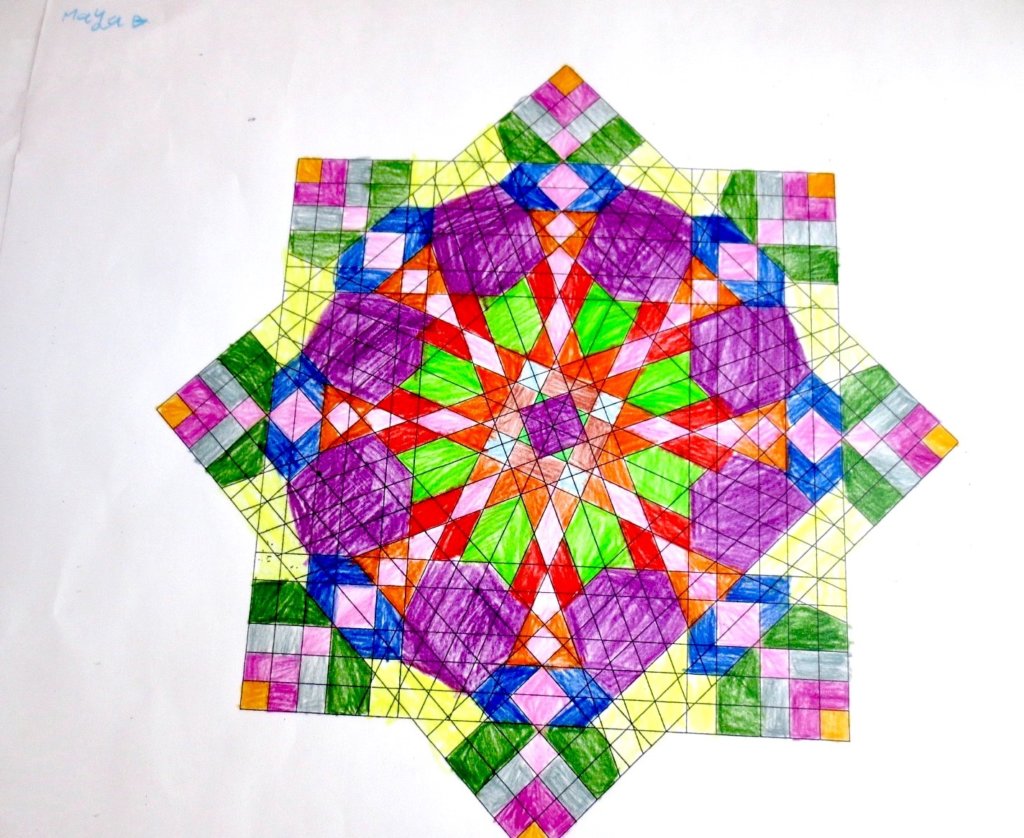
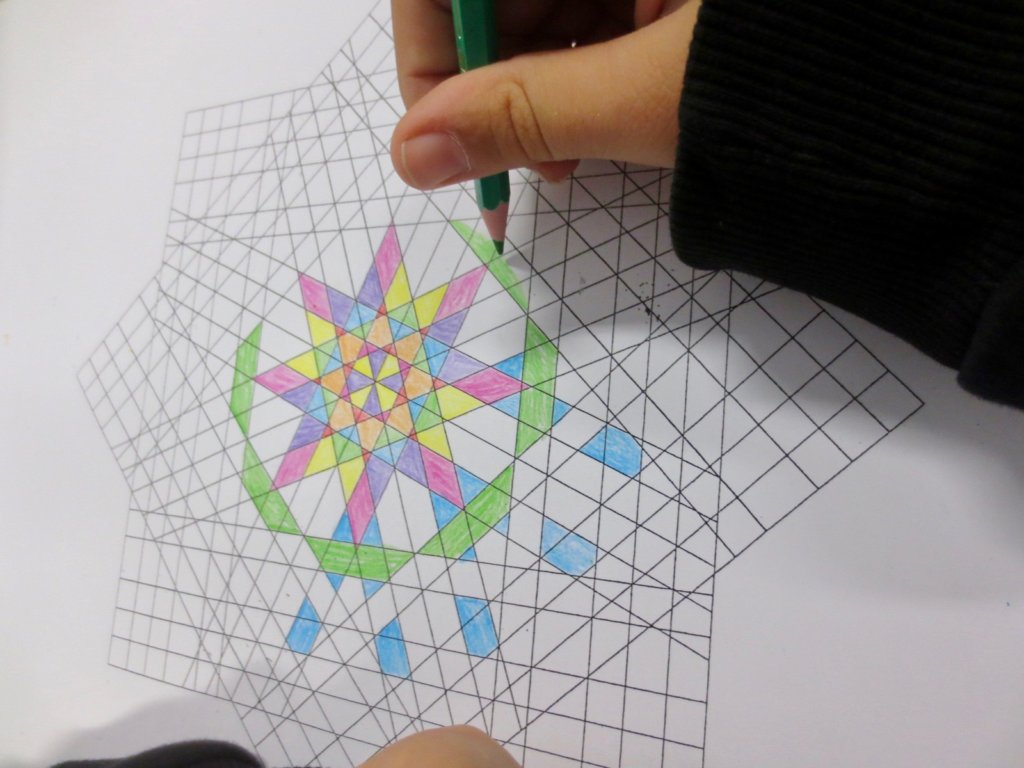
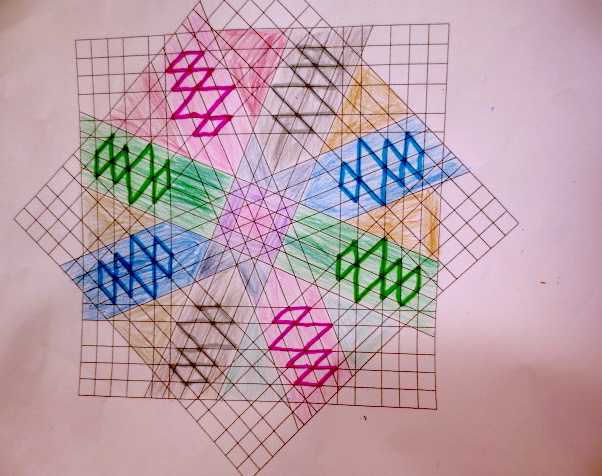Cada año los alumnos de quinto curso hacen un diseño teniendo como base la trama de Kamal.

Esta trama quizá hubiera estado en el olvido si no hubiera sido por que Karl Gertsner la descubrió en uno de sus viajes a la ciudad de Fez en Marruecos.

Gertsner, nacido en Suiza, en 1930, es uno de los artistas más importantes de su generación, sus obras, gran parte de ellas basadas en el diseño gráfico, han recorrido las salas de exposiciones y los museos más importantes.

Su preocupación fundamental estuvo centrada en descubrir las relaciones estructurales entre los diversos aspectos del universo visual, sobre todo la interacción existente entre forma y color. Para Gertsner, el color es luz (vibración electromagnética) y también es materia (sustancia química) y, además es percepción (dimensión fisiológica) y también sensación puesto que activa las emociones ( dimensión psicológica).

Si el color afecta a varias ciencias, la forma sólo es objeto de una: la geometría. La problemática estructural del color tiene que ver con la matemática, que tratará de ofrecer sistemas de ordenamiento y clasificación. Gerstner quiere hallar el sistema, la correlación estructural, la sintaxis que haga posible un discurso plástico unitario, donde forma y color sirvan al propósito de revelarnos sus relaciones y así procurarnos un genuino deleite, al mismo tiempo intelectual y sensual.

Fue Andreas Speiser, matemático de Basilea, quien inició a Gerstner en el arte islámico. A partir de ese encuentro Gerstner viaja y estudia sus monumentos y obras más significativas. En uno de esos viajes, en Fez, encuentra a un alarife —´arif— llamado Kamal Alí, a quien compra un diseño. A Gerstner se le ocurrió, a la vuelta de su viaje, introducir el patrón del diseño de Kamal Alí en un programa de ordenador. Su sorpresa fue tremenda cuando la trama reveló un número ilimitado de posibilidades estructurales y desarrollos formales. El humilde ’arif de Fez no le había vendido un diseño sino un patrón con capacidad para producir un número ilimitado de formas, una clave estructural, la semilla que habían guardado celosamente los mudéjares andalusíes expulsados durante la conquista del reino de Granada.   Gerstner comenta: “ …mi interés por el arte islámico se basa en que en él se ve realizado uno de mis sueños: un arte puro, una síntesis de purismo intelectual y un aura sensual».

Independientemente de los hechos históricos, debemos integrar todas las manifestaciones artísticas, que forman parte de un riquísimo legado cultural. Entenderemos nuestro presente si conocemos, entendemos y respetamos el pasado. En nuestra ciudad tenemos grandes muestras de un ecléctico y rico patrimonio cultural, conocerlo nos enriquece, como decía Gerstner,  obteniendo un sensitivo e intelectual deleite.

Nuestros alumnos hacen emerger mediante el color diseños únicos e ilimitados a través de este sistema de formas estructuradas geométricamente, a la vez conocen otras manifestaciones de su patrimonio cultural.

Ana Martín

La geometría surge con la necesidad de medir la tierra. Las relaciones numéricas en el plano y el espacio, se desarrollan con anterioridad a los símbolos numéricos. Los primeros geómetras entendieron las relaciones entre los números al observar el modo en que las formas geométricas se relacionaban entre sí.

El diseño geométrico prolifera en la actualidad como una divertida tendencia en la que bellos patrones muestran relaciones matemáticas de líneas rectas y curvas que desarrollan en el plano complejas relaciones. Esta moda del diseño geométrico se manifiesta en proyectos de moda, tatuajes, joyería,  sitios web, tarjetas, carteles.. A menudo es utilizado para crear motivos impecables, fondos abstractos y geniales efectos fotográficos.

La trama de Kamal es un patrón geométrico que ofrece a los alumnos la posibilidad de crear múltiples relaciones. Aplicando la simetría radial y mediante el coloreado de las diferentes formas los alumnos crean bellos y exclusivos diseños.

Las tramas funcionan como patrones estructurales del diseño geométrico.

Ana Martín

Os muestro los diseños que los alumnos de quinto han realizado mediante la decoración de la Trama de Kamal. Cuando les presento la plantilla y les digo que tienen que colorear, muchos de ellos protestan: «no me gusta colorear».  Les digo que no se trata solo de colorear. Para que las formas geométricas que subyacen en esta estructura emerjan tienen que usar el color, pero sobre todo la mente. Deben buscar la simetría, las relaciones entre los diferentes polígonos y hacerlos aflorar mediante el coloreado.

El espacio, la medida y las diferentes relaciones que se producen en el plano son los protagonistas de infinitas relaciones y que ellos tienen el poder de crearlos mediante el coloreado. Esto convence a la mayoría de los alumnos.

Este trabajo requiere gran concentración y esfuerzo y aunque no es necesario rellenar todos los espacios; unos se cansan y otros, aún rellenándolo todo, lo hacen de forma asimétrica.

Esta red modular fue custodiada con esmero por los mudéjares andalusíes durante el destierro de los hispanomusulmanes. Queremos que nuestros alumnos se introduzcan  en el funcionamiento de las redes modulares a través de esta trama.

Completamos la sesión con la decoración de otras redes modulares.

La práctica que habían hecho con la trama de Kamal, les ayudó para comprender las relaciones de simetría y las estructuras geométricas que se generan con estos patrones.

Los patrones modulares han sido utilizados en muchas ramas del diseño. Estas estructuras geométricas que generan multitud de posibilidades, tienen además la particularidad de poder teselar el plano. La teselación del plano mediante polígonos regulares constituye la base de la decoración de los zócalos de la Alhambra. Esta técnica de «alicatado» se sigue utilizando en la actualidad y forma parte de una herencia ancestral.  Es primordial que conozcan aquellas manifestaciones artísticas que forman parte de nuestro patrimonio cultural.

Ana Martín