Archivo de la etiqueta: Perímetros
Áreas y Perímetros
Problemas y ejercicios de áreas de polígonos
1.- Un campo rectangular tiene 170 m de base y 28 m de altura. Calcular:
a) Las hectáreas que tiene.
b) El precio del campo si el metro cuadrado cuesta 15 €.
2.- Calcula el número de baldosas cuadradas, de 10 cm, de lado que se necesitan para enlosar una superficie rectangular de 4 m de base y 3 m de altura.
3.- Hallar el área de un triángulo rectángulo isósceles cuyos lados miden 10 cm cada uno.
4.- El perímetro de un triángulo equilátero mide 0.9 dm y la altura mide 25.95 cm. Calcula el área del triángulo.
5.- Calcula el número de árboles que pueden plantarse en un terreno rectangular de 32 m de largo y 30 m de ancho si cada planta necesita para desarrollarse 4 m².
6.- El área de un trapecio es 120 m², la altura 8 m, y la base menor mide 10 m. ¿Cuánto mide la otra base?
7.- Calcular el área de un paralelogramo cuya altura mide 2 cm y su base mide 3 veces más que su altura.
8.- Calcula el área de un rombo cuya diagonal mayor mide 10 cm y cuya diagonal menor es la mitad de la mayor.
9.- En el centro de un jardín cuadrado de 150 m de lado hay una piscina también cuadrada, de 25 m de largo. Calcula el área del jardín.
10.- Calcula el área del cuadrado que resulta de unir los puntos medios de los lados de un rectángulo cuya base y altura miden 8 y 6 cm.
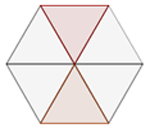
11.- Cuánto vale el área de la parte subrayada de la figura, si el área del hexágono es de 96 cm².
12.- Una zona boscosa tiene forma de trapecio, cuyas bases miden 128 m y 92 m. La anchura de la zona mide 40 m. Se construye un paseo de 4 m de ancho perpendicular a las dos bases. Calcula el área de la zona arbolada que queda.
13.- Un jardín rectangular tiene por dimensiones 30 m y 20 m. El jardín está atravesado por dos caminos perpendiculares que forman una cruz. Uno tiene un ancho de 8 dm y el otro 7 dm. Calcula el área del jardín.
14.- Dado el cuadrado ABCD, de 4 m de lado, se une E, punto medio del segmento BC, con el vértice D. Calcular el área del trapecio formado.
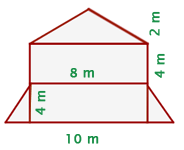
15.- Calcula la cantidad de pintura necesaria para pintar la fachada de este edificio sabiendo que se gastan 0.5 kg de pintura por m2.
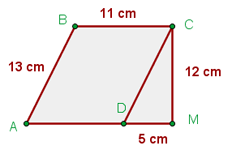
16.- Hallar el perímetro y el área de la figura: